The Department of Mathematics
Education
William
Daly
EMAT6680
Write Up #11
Summer
03
Straight Line in Polar Coordinates
Consider
the graph of the equation in polar coordinates:
![]()
For
many explorations in polar coordinates, we come to expect a symmetry or
periodicity about the origin. So why
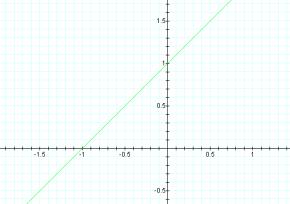
does this graph have the appearance of a straight line y=x+1 (in Cartesian
coordinates):
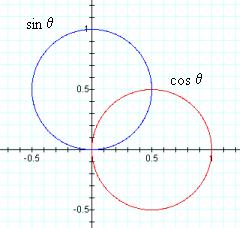
To begin this study, a natural starting point may be an understanding of each of the denominator terms, sinθ and cosθ. These are graphed over the range 0 < θ < π.
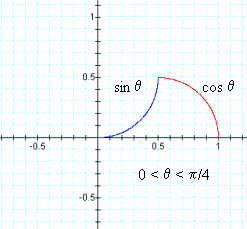
Plot these again from 0 to π/4 to get a sense of what each function is doing as θ. But it is clear that at θ=0, sinθ=0 and cosθ=1. Also θ=0, sinθ=0 and cosθ= π/2 sinθ=1 and cosθ=0. This explains the Cartesian points (-1,0) and (0,1).
At this
point is the development, we can observe a few points. Let the value of the denominator be d=sin θ – cos θ. It may be useful to graphs d(θ) to visualize the problem.
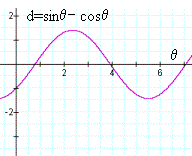
From looking at this graph of d(θ), it is clear that when θ=0, r=1/d=-1. Also, as θ approaches π/4 from the left, r → -∞; as θ approaches π/4 from the right, r → ∞. This occurs again at 5π/4. Note the θ =π/4 and θ =5π/4 corresponds to the line y=x+1, so that r→±∞ at these values of θ explains the linear behavior near θ =π/4 and θ =5π/4.
Now that the behavior at the
points(-1,0) and (0,1) as well as near θ =π/4 and θ =5π/4 shown to be
consistent with the line y=x+1, what about the remaining points near the
origin. There does not appear to be
anything intuitive about the graph of d(θ) nor the graphs of r=sinθ
and r=cosθ that would insist on the points in
the neighborhood of (-1,0) and (0,1) to lie on the line y=x+1.
To prove that this should be the case, it appears that
one ought to look toward the relationship between the Cartesian and polar
coordinate systems themselves. Recall
that:
x=r cosθ
and y=r sinθ
If
these are substituted into the original function, we obtain:
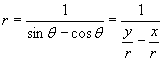
or ![]() .
.
After
canceling the r from both sides of the equation (note that r≠0), we are
left with:
y-x=1 or y=x+1.
