The
Department of Mathematics Education
William
Daly
EMAT6680
Write Up #2
Summer 03
Observations of Asymptotic Behavior Associated with
Adding nxy Term to a Quadratic
Starting with a quadratic function of the form y=ax2+bx+c,
a term nxy is added to this function. The
original quadratic is shown in Figure 1 with a=2, b=3 and c=-1.
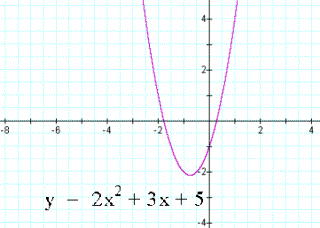
Figure 1: Original quadratic equation.
When adding the term nxy to this function, y=ax2+bx+c+nxy,
two obvious features of the resultant function is that the locus of points on
this new function always pass through the roots of the original quadratic and
through the point (0, -1) regardless of the value of n. This is demonstrated in the animation, Figure 2.
The cause of the behavior of always passing through
the roots of the quadratic is readily apparent by examining values of x for
y=0. Since this causes the added term
nxy to also be equal to zero, regardless of the value of n, we are left with
the original quadratic for y=0. Of
course, the solution to this is the roots of the original quadratic. The behavior of passing through the point
(0, -1) regardless of the value of n can be seen just as easily by noting that
the term nxy is again zero for x=0, are the second and first degree terms. This leaves the value “c”, or the point
(0,c). In our example, c=-1.
One additional very apparent feature is that the two
function coincide when n=0 for obvious reasons; n=0 is a third way to set the
nxy term to zero, but this holds for all x and y values. In other words, n=0 leaves us with the
original quadratic.
Beyond some of these immediately apparent features,
graphing the new function shows interesting behavior near the roots of the
original function. The remainder of
this paper explores this behavior.
In the example
y=2x2+3x-1+nxy, the graph bears a marked resemblance to y=+1/x,
as n approaches +∞, noting of course that the result is still
forced to go through the roots and (0,c) as previously mentioned. But there are a couple of critical
transition points that occur in the neighborhood of x=-0.56 and x=3.6 where the
“1/x” type graph abruptly changes from opening toward quadrants I / III to
opening toward quadrants II / IV. This
is demonstrated in Figure 3 for the neighborhood
of x=3.6..
This behavior becomes apparent by rearranging y=ax2+bx+c+nxy
as follows:
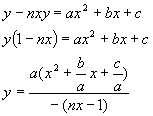
Assume the roots of the quadratic equation are r1
and r2. Then this equation can be
rewritten as:
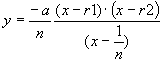
Note that the original quadratic is in the numerator of this result. It is now apparent what is occurring at the points x=-0.56 and x=3.6. Factoring the quadratic results in roots at r1=0.281… and at r2=-0.562…When n =1/r1=3.56 or n=1/r2=-0.56, terms cancel and the results becomes:
![]() or
or ![]()
Figure 4 and Figure 5 dynamically shows the new
functions behavior in the neighborhoods of the critical n values. Note that on either side of the critical
value, the linear portion of the graph agrees with the above description with
a slop of –a/n and a y intercept of
–(a·r1)/n = –a·r1·r2 = c. Note this is
already know to be a necessary result from earlier in our discussion when we
noted that this graph must always include the point (0,c). The two slopes are the just -a·r1 and a·r2.
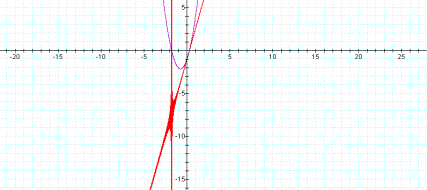
Figure 4: Transition point at root r1.
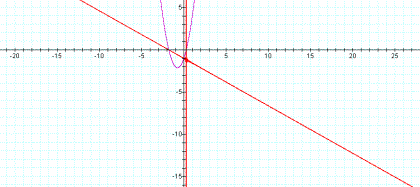
Figure 5: Transition point at root r2.
So now that the linear portion of the resulting
function is understood, what about the abrupt change in quadrants of the
resulting function? This is apparent
from noting the as x approaches1/n in the denominator (x approaches a root),
the denominator approaches zero from one direction, say positive. As x passes the root, the sign of the
denominator abruptly flip negative, hence the abrupt quadrant change of the 1/x
type result. Note also that the
vertical line at the root values on the x axis is undefined, strictly speaking,
since at this point, y=0/0.
To conclude, the addition of nxy results in 1/x type
graphs for values of n approaching infinity.
The behavior of the graph can be understood from considering the roots
of the original quadratic function. One
final note, if the quadratic is adjusted to not have any roots, the abrupt
transition behavior is absent from the animation as one might expect (see Figure 6).
