The Department of Mathematics Education

William Daly

EMAT6680

Write Up #4

Summer 03

Proof of Relationships Between the Medial

Triangle and Its Original Triangle

The following proof is based on a construction starting with equally spaced three parallel lines and intersecting lines, both parallel and at arbitrary angles. As the construction proceeds, it is seen that the result is one side of the medial triangle within its original triangle. The proof is done considering one side of the medial triangle, but identical arguments apply as the main triangle is “turn onto” each of its sides.

The relationships to be proven are:

- Each side of the medial triangle is parallel to the opposite side of the original triangle.

- Each side of the medial triangle is half the length of the opposite side of the original triangle.

- The medial triangle is similar to the original triangle.

- The medial triangle is one fourth the area of the original triangle.

Construct a vertical segment and its midpoint:

Construct three lines perpendicular to these point. These lines are parallel to each other and equally spaced:

Construct a line through B at an arbitrary angle, which intersects the top parallel line at D and the lower parallel line at E:

Construct a line through D at an arbitrary angle, intersecting the lower parallel lines at F and G:

Construct segments perpendicular to the original three parallel lines through D and F:

Define EDG as the original triangle under consideration.

Prove each side of the medial triangle is parallel to the opposite side of the original triangle.

Recalling that the original parallel lines are equally spaced, AB=BC. EAB and DCB are right angles by construction. Since the interior angles, BEA and BDC, at the intersection of ED with the three parallel line are equal, the triangles EAB, BJD and DCB are congruent. Therefore EB and BD are equal length and B is the midpoint of ED.

A similar argument shows GF and FD are equal length and F is the midpoint of GD. Also GIF, FJD and DKF are similar. Furthermore, GI=FJ.

Since it has been shown that EB=BD and GF=FD, the segment BF is one of the medial triangle legs of the original triangle EDG. Also BF is parallel to EG by construction, therefore the side BF of the medial triangle is parallel to the opposite side EG of the original triangle

Prove each side of the medial triangle is half the length of the opposite side of the original triangle.

To prove that the opposite side of the original triangle is twice the length of the medial triangle note that in the last section it was proven that the triangles EAB, BJD and DCB are congruent . Therefore the leg EA=BJ and GI=FJ. Since BJ+FJ is the length of the medial leg BF, EA+GI is also the length of the medial leg BF. Also AI is the length of the medial leg BF. Therefore medial triangle leg BF is half the length of EA+GI+AI, which is the leg EG of the original triangle.

Prove that the medial triangle is similar to the original triangle.

The previous proofs show that one leg of the medial triangle is parallel to and one half the length of the opposite leg. An identical proof on each side of the main triangle proves this for all side of the medial and main triangle. Therefore, since all legs of the medial triangle are parallel to the opposite side, the medial triangle constructed within the main triangle forms three parallelograms:

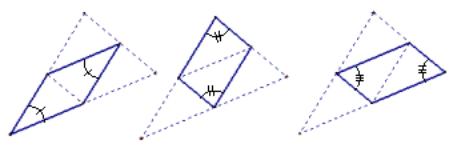
Note that the opposite angles in each of these three parallelograms are congruent and in each case one of the angles is the main triangle, and the opposite congruent angle is the medial triangle. Therefore, the medial and original triangles are similar.

Prove that the medial triangle is one fourth the area of the original triangle.

Note that is has been proven above that the medial triangle and the original triangle are formed by three pairs of parallel lines. As a consequence of this, the following angles are all congruent:

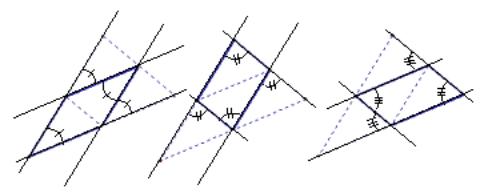
This construction breaks the original triangle into four individual triangles, one of which is the medial triangle. In the above sketch, it is shown that each of these four triangles is a least similar. But it was shown in an earlier proof that the legs of the medial triangle are congruent to each of the opposite mid point segments. Therefore all four of these triangles, are congruent and equal area, hence the medial triangle area is one fourth the total.

Return