The Department of Mathematics
Education
William Daly
EMAT6680
Write Up #8
††††††††††† Summer
03
Altitude
Relationships to the Circumcircle and Orthocenter
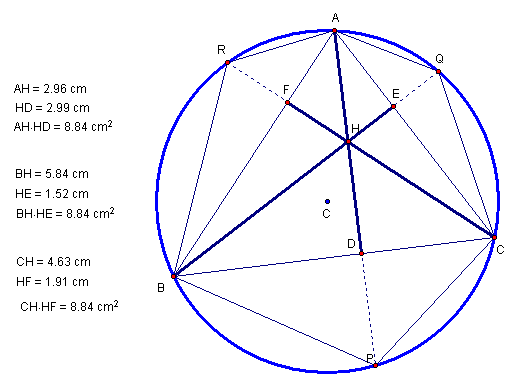
Shown below is an arbitrary acute triangle.† The construction of the altitudes and circumcircle
are shown.† Using GSPís measurement
tools, it is demonstrated that the product of the two segments of the altitude
on either side of the orthocenter is the same constant value for all three
altitudes of the triangle.† Throughout
this proof, several other similarities of the inscribed figures are discovered.
To
prove this relationship, first consider just one of the altitudes:

The
triangle BPC segments were included in this figure.† Notice that there are several chords in this diagram subtended by
two angles with vertices on the circumcircle.†
These angles are equal.† So for
chord AB –ACB=–APB.†
For chord BP –BAP=–BCP.†
For chord PC –BPC=–PAC.†
Finally for chord AC –CPA=–CBA.†
With these equal angles, it is clear that BDA@PDC and ADC @BDP.† This is shown below with similar triangles
shaded in the same colors.

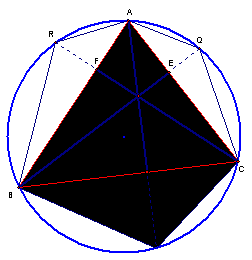
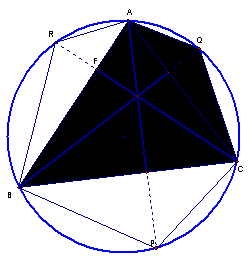
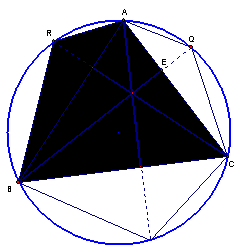
This
argument is applied to each of the perpendicular lines, leading to the
following similar triangles.† All of the
chords are drawn in this figure.† The
figure replicated three times to make the similar triangles more visible.
 †
† †
†
There
are additional similarities among these figures.† For example –DBA=–CBF appears in both the first and third figures,
and these two triangle have a right angle at points D and F respectively.† So –BAD=–BCF.†
But from the similar triangles above, both of these are also equal to
DCP.† This argument applied to the other
pairs of figures, 1,2 and 2,3, shows that the remaining triangles in white are
similar to each of their reflections about†
chords AB, AC and BC, the legs of the original triangle.† This also proves that the length of PD=DH,
QE=EH and RF=FH.† The relationships
shown below follow from consider the same relationships among the similar angle
between the figures above.
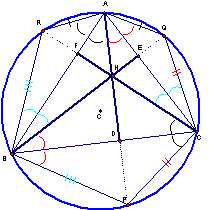
Considering
similar triangles from the blue, black and red congruent angles above, it is
clear that:
![]() †;
†; ![]() †;
†; ![]()
Apply
a shorthand notation to the segment lengths.†
Each one will be the distance from the point H.† So AH becomes A, BH become B, etc.†
Then
AD=CF=BE.† That is the product of the
two segments of the altitude on either side of H is a constant.
