The Department of Mathematics Education

William Daly

EMAT6680

Write Up #9

Summer 03

Degenerate Pedal Triangle – The Simson Line

The pedal triangle, formed from the perpendiculars to the extended legs of the main triangle, forms a degenerate triangle. This degenerate triangle can be thought of as having two angles of 0º and one angle of 180º. In other words the vertex to the altitude lies on the base and the altitude is zero. In this case the pedal triangle is a line segment with all vertices lying on the segment. This line segment is called the Simson Line. Shown below are three cases of a pedal triangle. First is an arbitrary pedal point and pedal triangle. The second figure shows a case where the altitude of the pedal triangle is reduced and the third case shows where this altitude is finally reduced to zero. Click on Figure 1 to observe the pedal point merge from an arbitrary triangle to the degenerate case.

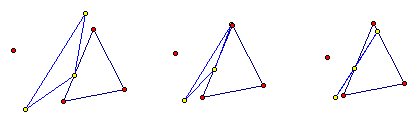
Figure 1: Progression from arbitrary triangle to degenerate case.

What are the conditions required for the existence of the Simson line? One conditions that appears to be obvious is where the pedal point is coincident with one of the vertices of the original triangle from which the pedal triangle was constructed. Recall that the pedal triangle is constructed from connecting the perpendicular intersections with the original triangle’s extended sides. If the pedal point is coincident with any vertex of the original side, then the perpendicular to these sides of the triangle is of zero length. Thus the resultant triangle will be degenerate. In fact this is a unique case of the Simpson line in that one of the degenerate side is zero length and two of the vertices of the degenerate triangle are coincident. Also note that in this case the Simpson line is also an altitude of the original triangle. Click on Figure 2 to observe the triangle degenerate as the pedal point moves to the vertex.

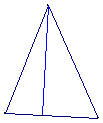
Figure 2: Simpson line for pedal point at a vertex of the original triangle.

For cases other than at the vertex, toying with the pedal point reveals that for it to cause a degenerate triangle, some sort of a curve is followed we the pedal point moves from one vertex to the other. Without proof, one may suspect that this sounds like it may be the circumcircle of the original triangle. Figure 3 shows the original triangle with the circumcircle. The first case is where the pedal point is outside the circumcircle, the second has the pedal point inside the circumcircle and finally, the pedal point is on the circumcircle. Clicking on Figure 3 reveals that as the pedal point traces out the circumcircle, all of the resultant pedal triangles are degenerate.

Figure 3: Positioning the pedal point for a degenerate pedal triangle.

Return