

To start this investigation, I will choose any two linear functions. I will start with
I also need to find f(x) + g(x) to get h(x). So,
Now, I will graph f(x) in blue, g(x) in red, and h(x) in green.
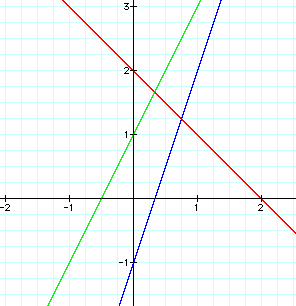
As you can see, h(x) is also a linear function. This is true for any two linear functions because when you add two linear functions, x will either keep the same degree or it will cancel out. If x does cancel out, the sum, h(x), will be a constant, which is still linear. The degree of x will never increase. As a matter of fact, when adding any number of linear functions, the sum will still be a linear function.
Here, I am going to investigate the product of two linear functions. I will use the same functions as before:
I also need to find the product, h(x).
Now, I will graph f(x) in blue, g(x) in red, and h(x) in green.
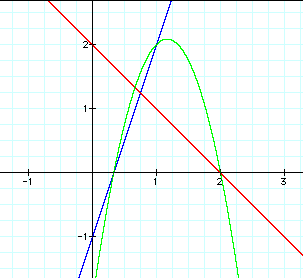
As you can see, h(x) is a parabola, or a quadratic. The product of two linear functions will always be a quadratic because when multiplying, the degree of x will always increase to 2.
Another observation is that the x-intercept of f(x) and g(x) are where the roots of h(x) occur. This will also always be true. Since h(x) is the product of two linear functions, then it will have two roots. Thus, if you multiply three linear functions together, the product will have three roots and the degree of h(x) will be three; if you multiply four linear functions together, the product will have four roots and the degree of h(x) will be four, etc. In general, if you multiply n linear functions together, the product will have n roots and the degree of h(x) will be n.
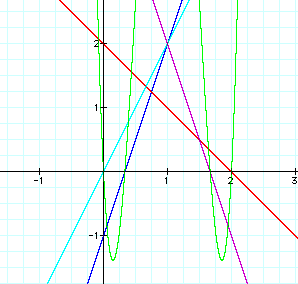
Below is an example of multiplying four functions together, where the product j(x) is in green.
The product is:
In the graph below, f(x) is dark blue, g(x) is red, h(x) is light blue, i(x) is purple, and j(x) is green.
Now, Iwill investigate the quotient of two linear functions. Again, I will use the same f(x) and g(x).
The quotient is:
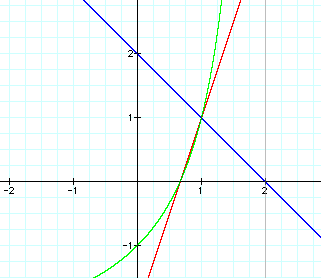
From observing the graph above, you can see that the quotient, h(x), is a rational function. There is an asymptote at x=2.
This time, I am going to look at the composition of f(x) and g(x). Because of functions we chose for f(x) and g(x), there are some special relationships between the three functions.
The composition f(g(x)) is:
Below, f(x) is blue, g(x) is red, and h(x) is green.
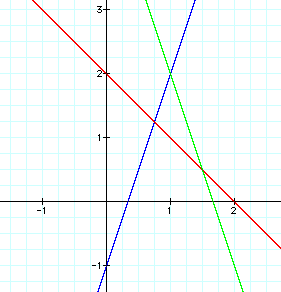
The composition function, h(x), is a linear function. This will always be true because we are simply taking a linear function and multiplying it by a constant and adding a constant. Thus,every h(x) that is a composition of two linear functions is also a linear function.