

Generate a Fibonacci sequence in the first column using f(0) = 1, f(1) = 1,
Click here to get a spreadsheet of the first 50 terms in Fibonnaci's sequence.
a. Construct the ratio of each pair of adjacent terms in the Fibonnaci sequence. Click here for this spreadsheet. (At the bottom of the spreadsheet, there is a button that is labeled "Ratio of Fib Numbers." If you click on it, you ill see a chart that has graphed the Ratio of Fibonnaci Numbers). In case you have trouble, here is a picture of the graph.
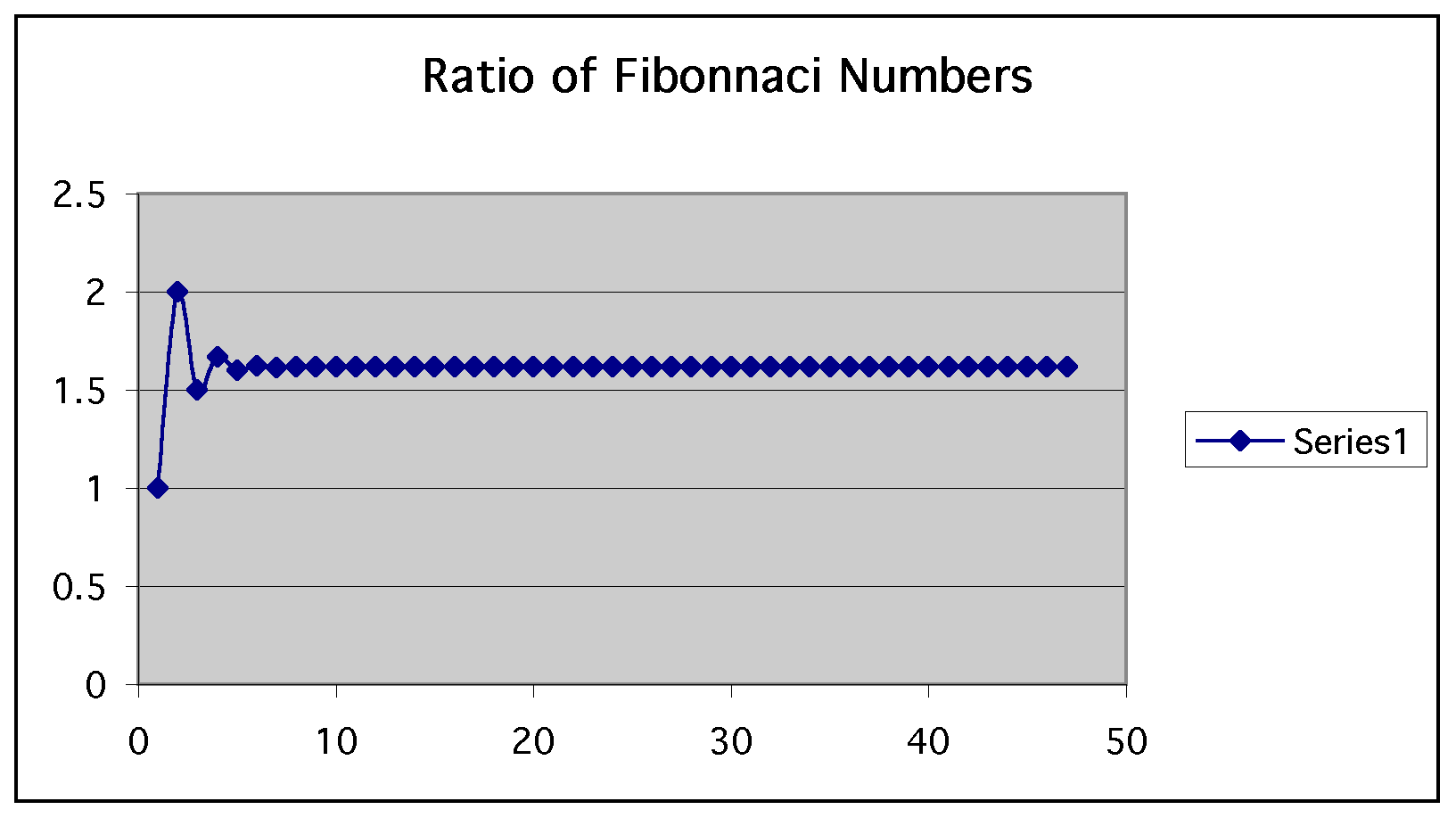
As you can see in the graph and even better in the spreadsheet that as n increases, the sequence is reaching a limit at approximately 1.61803399. Have you seen this number before? YES!! It's Phi, or the golden ratio.
Construct the ratio of every second term. Click here for this spreadsheet. Again, there is a graph attached to this.
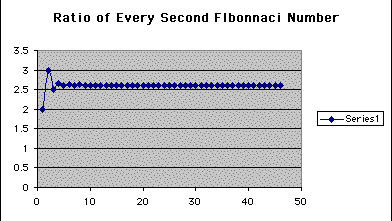
Again, you can see in the graph and even better in the spreadsheet that as n increases, the sequence is reaching a limit at approximately 2.61803399, or Phi + 1.
b. Explore the sequence hen f(0) and f(1) are different.
Let's try f(0)=1 and f(1)=3. This is called the Lucas sequence. Click here for a spreadsheet of the first 50 terms in Lucas' sequence.
Construct the ratio of each pair of adjacent terms in Lucas' sequence and every second term in the sequence. Click here for the spreadsheet that contains both ratios.
This is the graph of the sequence of ratios of adjacent terms in Lucas' sequence.
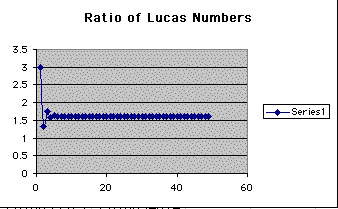
Again, as n gets larger, the sequence reaches a limit at 1.61803399, or phi.
Here is the graph of the sequence of ratios of every second term in Lucas' sequence.
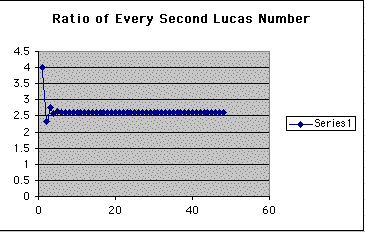
And again, as n gets larger, the sequence reaches a limit at 2.6103399, or phi + 1.
By further investigation, I have realized that these ratios are going to alays reach these same limits. Thus, I conclude that for the sequence
for any f(0) and f(1), the ratio f(n)/f(n-1) alays reaches a limit of 1.61803399, or Phi, and the ratio f(n)/f(n-2) alays reaches a limit of 2.61803399, or Phi + 1.