

In high school Algebra, students begin to learn about quadratic equations. Usually, the teacher introduces quadratic equations by showing the students what the equation looks like and what the graph looks like. The teacher might then give the students an excercise that deals with changing the coefficients to see how the graph changes. The students would probably approach this type of problem by making a t-chart of x and y values. But, it has now become a rather standard exercise, with availble technology, to construct graphs to consider the equation
and to overlay several graphs of
for different values of a, b, or c as the other two are held constant. From these graphs discussion of the patterns for the roots of
can be followed. In order to explore the effects of one variable at a time, set a nd c to be held constant. For example, let a = 1 and c = 1. So, we will set
for b = -3, -2, -1, 0, 1, 2, 3, and overlay the graphs on the same screen of their calculator, the following picture is obtained.
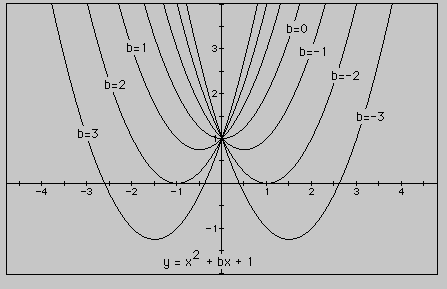
We can discuss the "movement" of a parabola as b is changed with the students referring to this screen. The parabola always passes through the same point on the y-axis (in this case, the point (0, 1)). When b is less than or equal to 2, the parabola will intersect the x-axis in two points with positive x values. When b is equal to the absolute value of 2, the parabola is tangent to the x-axis. For b between, but not equal to, -2 and 2, the original equation has no real roots; that is, the parabola does not intersect the x-axis. Finally, for b larger than 2, the parabola will intersect the x-axis twice to show two negative real roots for each b.
Now, the students should observe the locus of the vetices of these parabolas. If the students do not know what a locus is, then the teacher should instruct them to graph the vertices of all of the parabolas and connect the points to obtain the locus. Below, you can see the locus of the vertices.
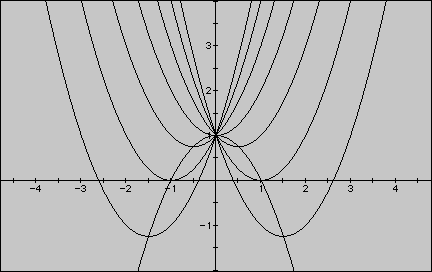
The equation of the locus of theses vertices is the parabola
After discussing the basics of a parabola, the students should be able to come up with this equation, where a=-1, b=0, and c=1. The next question would be, "What is the equation for the locus of the vertices of a different set of parabolas?"
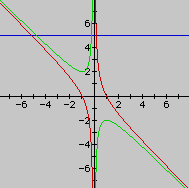
Consider again the equation,
This time, we are going to graph the equation in the xb plane. Students might be confused by the meaning of an xb plane. All that they need to do is replace every b with a y, and then graph it the same way on a graphing calculator. We will get the following graph:
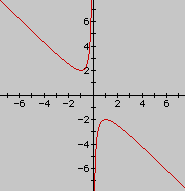
With this graph, we are able to see the roots of the equation. For example, if we take any particular value of b, say b = 3, and overlay this equation on the graph we add a line parallel to the x-axis. If it intersects the curve in the xb plane the intersection points correspond to the roots of the original equation for that value of b. We have the following graph.
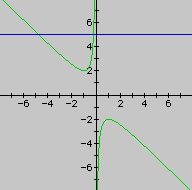
You can see that there are two negtative roots, and the students could approximate these with an educated guess. My approximation is x = -5 and -1.
It is clear on a single graph that we get two negative real roots of the original equation when b > 2, one negative real root when b = 2, no real roots for -2 < b < 2, One positive real root when b = -2, and two positive real roots when b < -2.
The next step would be to consider the case when c = - 1 rather than + 1. Now, how many roots are there when b > 2, b=2, -2 < b < 2, and b < -2 ?
Let's consider the equation
We want to graph this equation in the xc plane. In order to do this on the graphing calculator, you need to substitute a y in for every c, and then graph as usual. If the equation is graphed in the xc plane, it is easy to see that the curve will be a parabola. For each value of c considered, its graph will be a line crossing the parabola in 0, 1, or 2 points -- the intersections being at the roots of the original equation at that value of c. Below is an example when c = 1. So, we'll graph the equation
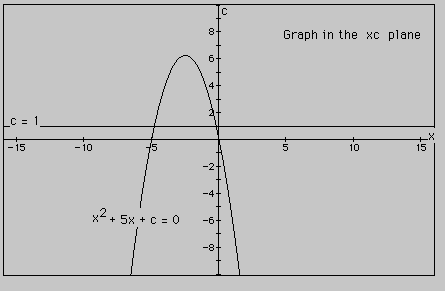
As you can see, the equation ![]() has
two negative roots -- approximately -0.2 and -4.8.
has
two negative roots -- approximately -0.2 and -4.8.