

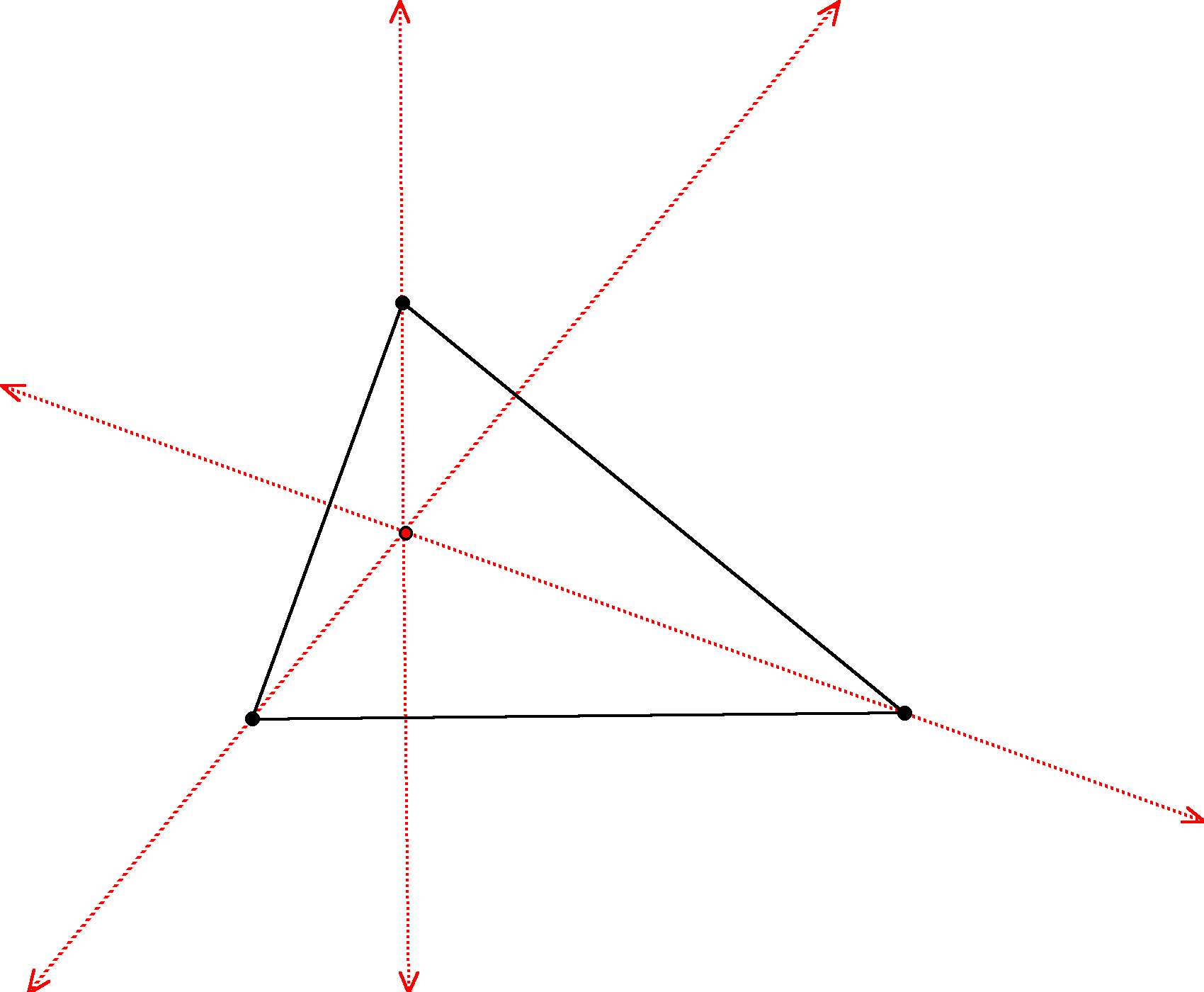
To begin this proof, I will construct lines through each vertex that is perpendicular to the opposite side. Then, construct their points of intersection.
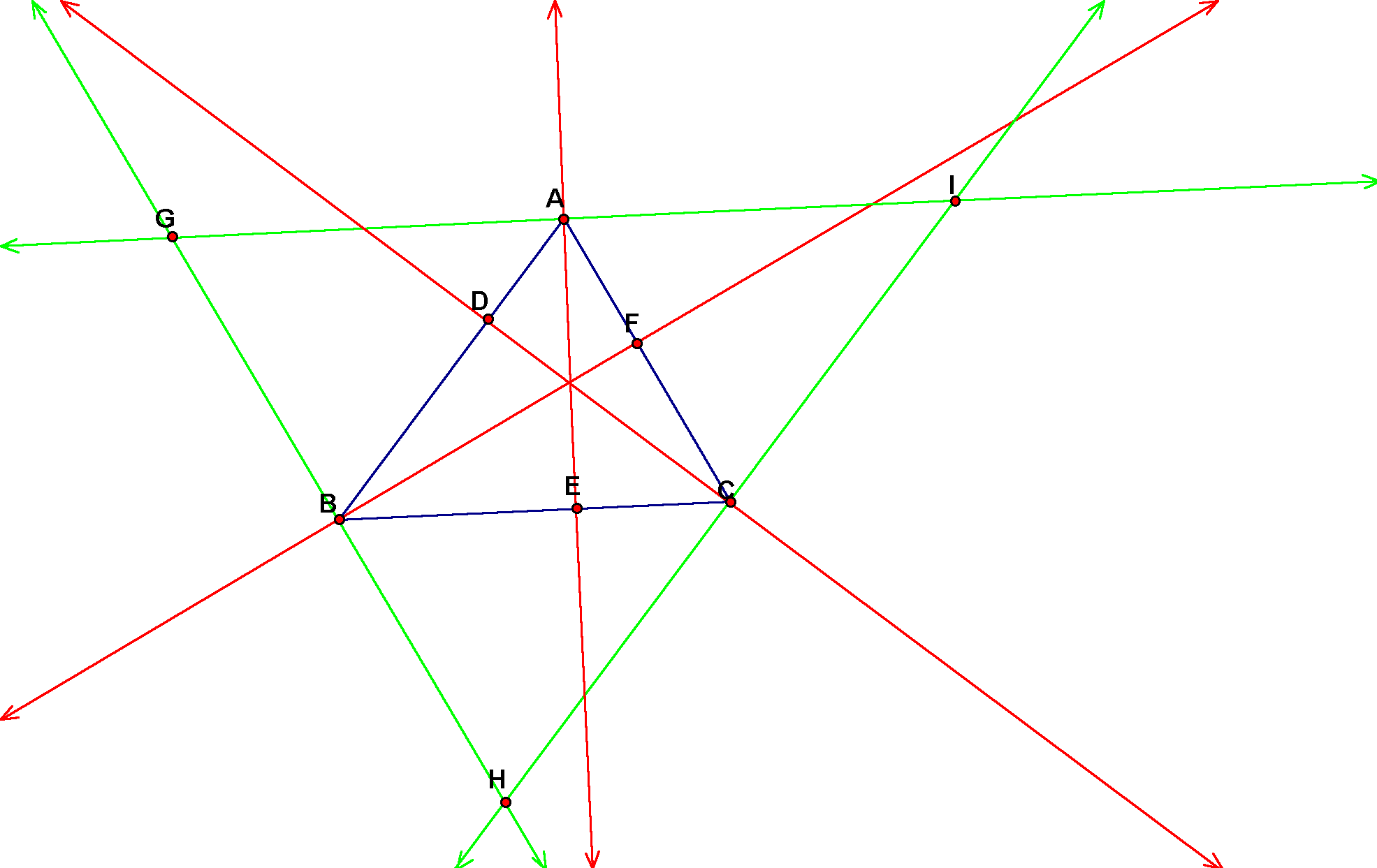
First we must prove that the altitudes of the
small triangle ABC are the perpendicular bisectors of the larger
triangle GHI. By construction, we know that segment BA is parallel
to HI and by construction we also know that GI is parallel to
BC. Since the definition of a parallelogram is that it has two
sets of parallel sides, we know that BCAI must be a parallelogram.
One of the properties of a parallelogram is that opposite sides
are congruent, so BC=IA. By construction, we also know that AC
is parallel to GB, so by difintion of parallelogram, GABC must
be a parallelogram. So BC=GA by the properties of a paralleogram.
Since both IA and GA are equal to BC, IA=GA.
Similarly, HC=CI and HB=BG.
So we have proven that the altitudes bisect the sides of the larger
triangle, now we must prove that the altitudes are perpendicular
to the sides of the larger triangle. Since GI is parallel to BC,
and AE is the altitude of BC, which means it is perpendicular
to BC, therefore AE must also be perpendicular to GI. Sinilarly,
CD is perpendicular to HI, and BF is perpendicular to GH.
Now we have proven that the altitudes of the smaller triangle
ABC are the perpendicular bisectors of the larger triangle GIH.
We know that the perpendicular bisectors of a triangle are concurrent
(for proof, click here),
so the altitudes must also be concurrent.
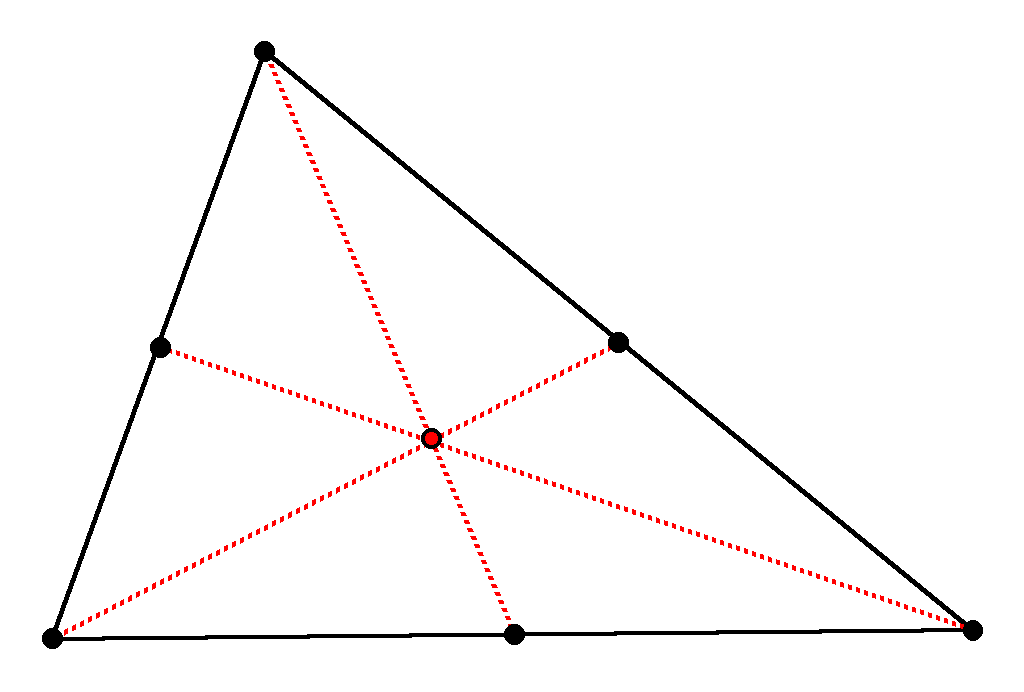
To do this proof, I will construct two triangles, Triangle1 and Triangle2.
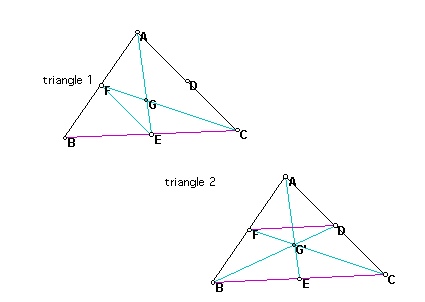
Triangle 1:
Triangles BEF and ABC are similar by Side Angle
Side Congruence theorem because they share the same angle B and
their sides have a ratio of 1:2 because of the existance of midpoints.
So we know that the ratio of FE to CA is 1:2. Now we can prove
triangle FEG is similar to GCA by Angle Angle Angle because angle
FGE=angle CGA since they are vertical angles and vertical angles
of intersecting lines are congruent, and angle GFE=angle ACG and
angle CAG=angle GEF because alternate interior angles of parallel
lines are equal. We know that FE is parallel to CA by the converse
to Euclide's theorem book 6 prop.2. Since FGE is similar to AGC,
we know that all sides must have the ratio of 1:2, therefore FG:GC
is 1:2.
Triangle2:
I kept the line FC the same, but I added line
BD. We know all of the points F,D,E are the same because they
are the midpoints, but we aren't sure that G is the same point
so we rename it G'. If we can prove that G and G' are the same
point, we will prove that all three lines are concurrent. We prove
that triangle FDG' and triangle BCG' are similar by the same process
above (Angle Angle Side similarity theorem). So we know all the
sides have the ratio 1:2. Therefore FG':G'C is 1:2, so that means
G'=G. Therefore, all three lines are concurrent.