12. Prove that the perpendicular bisectors of a triangle are concurrent.

In order to begin this proof, I constructed the segments from the point of intersection to the vertices. These are the segments that I am trying to prove are equal. I also constructed segments from the midpoints to the point of intersection as well. And, in order to speak clearly, I will label the points.

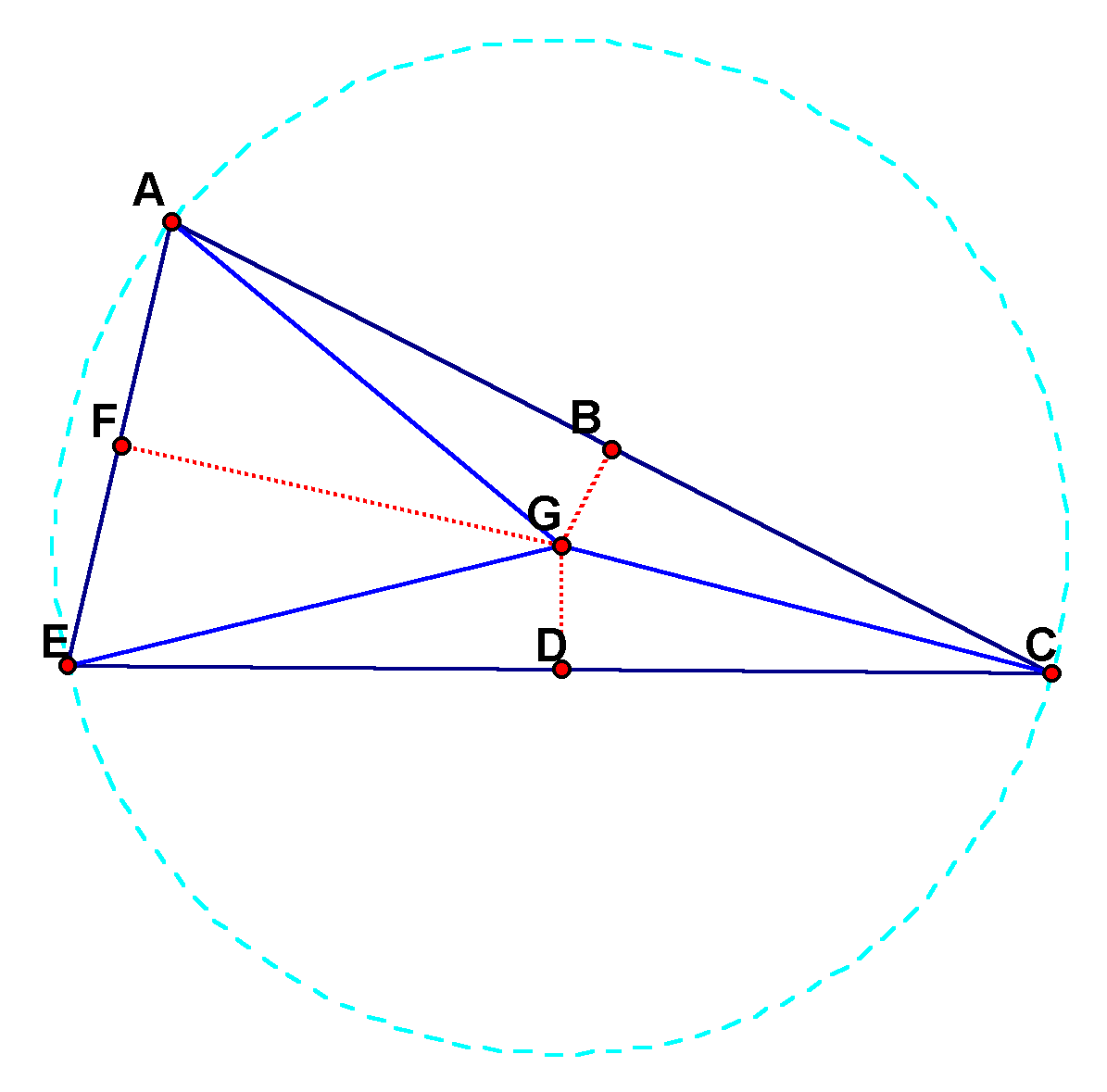
I know that:

BG=BG from the reflexive property,
AB=BC from the definition of perpendicular bisector (B is the bisector of AC)
Angle(ABG)=Angle(CBG)=90 degrees from the definiton of perpendicular bisector (BG is perpendicular to A.

So, by Side-Angle-Side Congruence,

By CPCTC,

AG = GC

Likewise,

By CPCTC,

GC = GE

GE = GA respectively

Thus,

AG = GC = GE.