

The center of the desired circle will lie along a line from the center of the given circles with the specified point.
Next, you must find the point that is the length of the radius of the other circle from the specified point.
Now, construct a segment between this point and the center of the other circle. Find the perpendicular bisector of this line. And construct the intersection point of the perpendicualr bisector and the original line.
Now, construct the tangent circle.
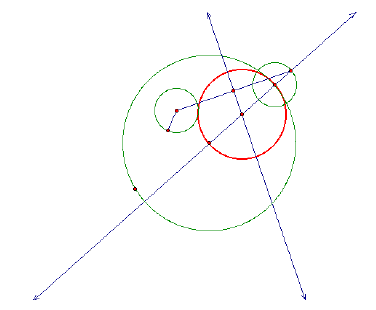
For simplicity purposes, I will hide all of the construction items.
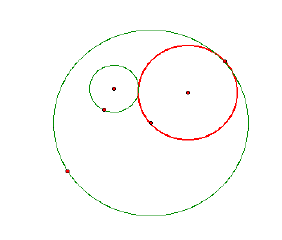
1. Make a script tool for the construction of the tangent circles.
2. The following constructed tangent circle is not one of those in the investigation so far. Make a script tool for the generating this case.
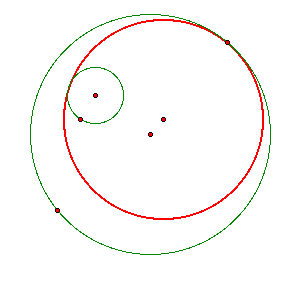
3. Use your script tools to construct the tangent circle to two given circles if the given point is on the smaller of the two circles
a. so that the smaller circle is external to the tangent circle.
b. so that the smaller circle is internal to the tangent circle.
These constructions are not hard! It is the exact same process as when the point is on the bigger circle, except the circles are switched!
4. Discuss the loci of the centers of the tangent circles for all case you construct.
Consider the locus of the center of all such circles tangent to the two given circles. With GSP, we can animate around the circle and trace the locus of the center as follows:
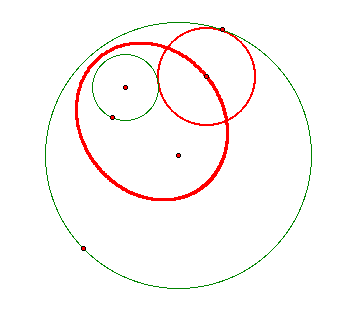
To see this animation with GSP, click here.
If the center of the constructed circle is connected by segments to the centers of the two given circles, it is immediate that the sum of the segments is the same as the sum of the radii of the two given circles. This sum is a constant and therefore the locus of the centers of the tangent circles is an ellipse with foci at the centers of the given circles.
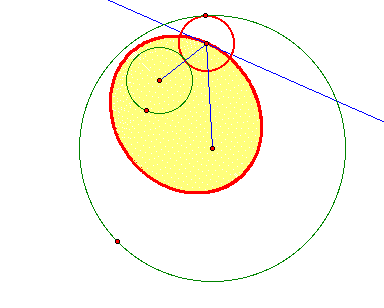
The blue line in the picture, that is in your construction, is always tangent to the locus--the ellipse. Do a trace of the line as the tangent point of the constructed circle moves around the large circle. An envelope of lines is produced all tangent to the ellipse. This is essentially the underlying technique of folding wax paper to define an ellipse by the envelope of folds.

To see this animation with GSP, click here.
5. Discuss the constructions of the tangent circles if the two given circles intersect.
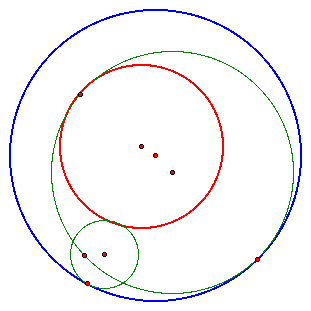
The construction of these circles is the same as the original constructions. You can go back to those scripts and just move the smaller circle to a place where it is intersecting with the bigger circle.
As you can see, now the second tangent circle (blue) is tangent to both of the given circles on the outside. Whereas before, it was tangent to the smaller circle on the outside and the bigger circle on the inside.
6. Discuss the locus of the centers of the constructed tangent circles when the two given circles intersect.
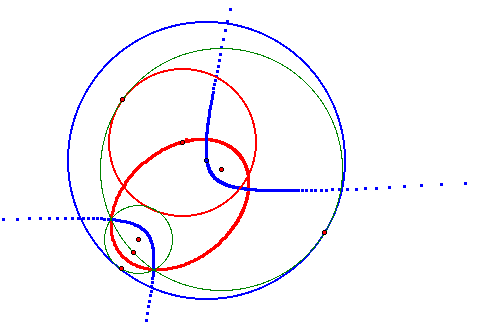
As you can see, the locus of the center of the red circle is still an ellipse (which I discussed before). But, the locus of the center of the blue circle is a hyperbola, where the focus of each side is the center of one of the given circles.
To see this animation with GSP, click here.
8. Discuss the construction of the circles tangent to two given circles when two circular regions are disjoint.
Here are a few cases:
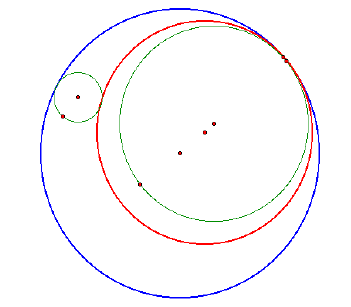


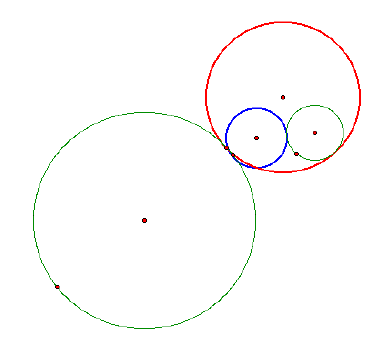
As you can see, the blue and red circles, flip when the smaller given circle is moved around the bigger given circle. At some point, the blue circle is disjoint and becomes a line before it flips to the other direction. (Same for the red circle, but at a different time).