

1. Construct any triangle ABC.
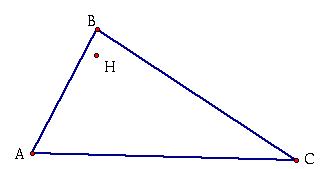
2. Construct the Orthocenter H of a triangle ABC.
3. Construct the Orthocenter (E) of triangle HBC.
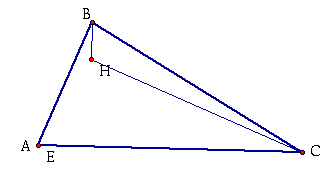
As you can see, the orthocenter of HBC is the left out vertex of the original triangle, A. So, A=E.
4. Construct the Orthocenter (F) of triangle HAC.
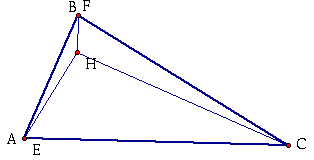
Again, you can see that the orthocenter of HAC is B. Thus, B=F.
5. Construct the Orthocenter (G) of triangle HAB.
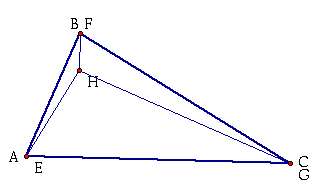
And again, we got the same result. The orthocenter of HAB is C. So, C=G.
6. Construct the Circumcircles of triangles ABC, HBC, HAB, and HAC.
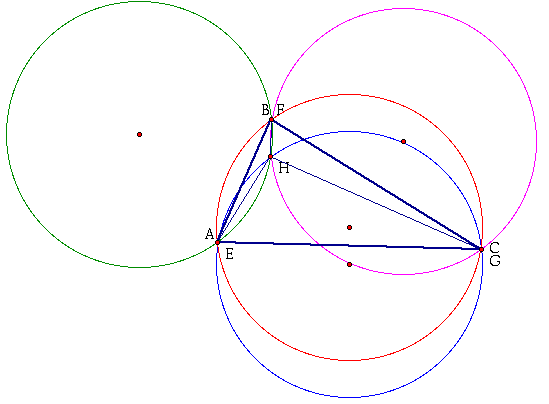
For a script in GSP that will do all of these steps in one step, click here.
In the picture above, you can see that the circumcircles of HAB, HBC, and HAC all concur at the orthocenter H of the triangle ABC. This is always true!
What would happen if any vertex of the triangle ABC was moved to where the orthocenter H is located? Click here to see these animations using GSP. As you can see after observing these animations, when A moves toward H, then H moves to where A was. The same thing happens with B and C. The triangle looks the same when these two points have replaced one another.
8. Construct the nine point circles for triangles ABC, HBC, HAC, and HAB.
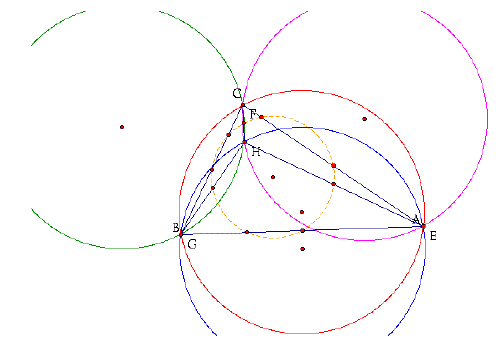
Click here for a GSP script of this construction.
In the picture above, you can only see one nine point circle. The reason for this is that the nine point circle for triangles ABC, HAB, HBC, and HAC are all the same!