

1. Let triangle ABC be any triangle. Then if P is any point in the plane, then the triangle formed by constructing perpendiculars to the sides ABC (extended if necessary) locate the three points R, S, and T that are the intersections. Triangle RST is the Pedal Triangle for Pedal Point P.
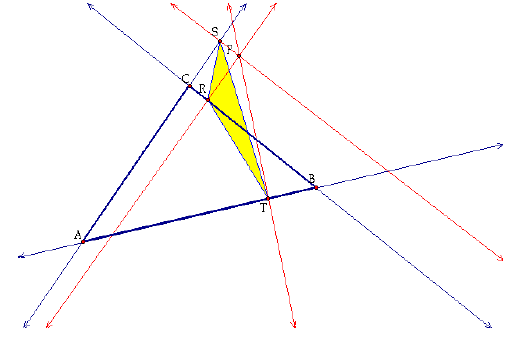
Click here for a script tool for the general construction of a pedal triangle to triangle ABC where P is any point in the plane of ABC.
10. Locate the midpoints of the sides of the Pedal Triangle (X, Y, and Z). Construct a circle with center at the circumcenter (K) of triangle ABC such that the radius is larger than the radius of the circumcircle.
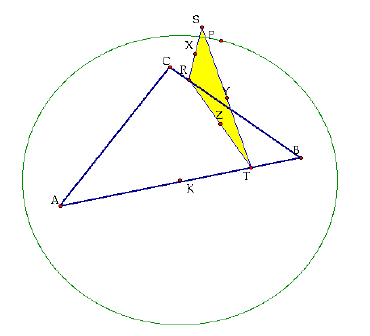
Trace the locus of the midpoints of the sides of the Pedal Triangle as the Pedal Point P is animated around the circle you have constructed.
X = red
Y = green
Z = purple
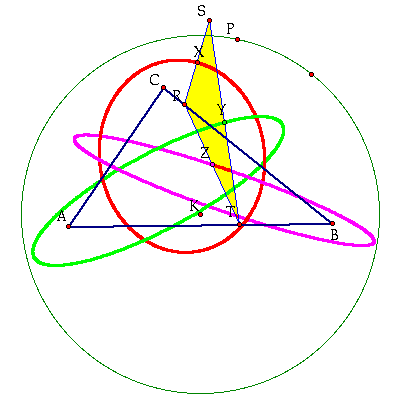
As you can see, the paths of the midpoints as P animates around the constructed circle are all ellipses. It seems to appear as though A, B, and C are foci of these ellipses, but after further investigation, you can see that they are not. It is true though that A will always be inside the green ellipse, B will always be inside the purple ellipse, and C will always be inside of the red ellipse.
Click here for the animation with GSP.