What is a parametric curve?

A parametric curve in the plane is a pair of functions

x= f(t)

y=g(t)

where the two continuous functions define ordered pairs (x,y). These two equations are usually called the parametric equations of a curve. The extent of the curve will depend on the range of t. We wil pay close attention to the range of t in our investigations.

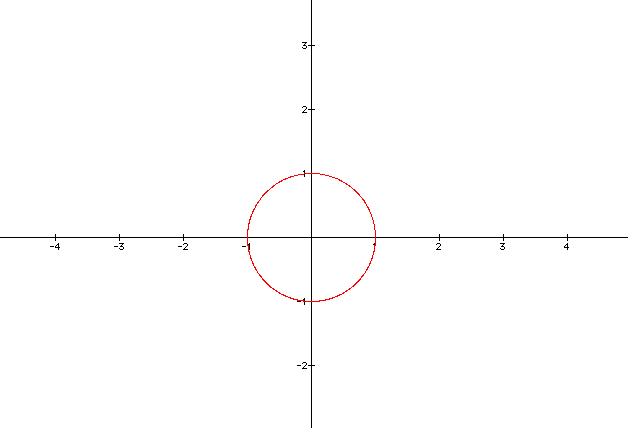
Graph x= cos(t) and y=sin(t) for 0<t<2pi

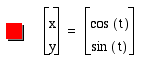
As you can see, these pair of functions produce a parametric curve that is a circle with a radius of 1.

Now, let's do some changes to this graph and see some other transformations!

x=cos(at)

y=sin(bt) for different values of a and b.

We are still dealing with t between 0 and 2pi.

Note: When a and b = 1, we get the graph that we started with! Let' s check out what happens for values other than 1.

I noticed something really interesting. As long as a and b are equal, they produce the same graph that x=cos(t) and y=sin(t) did, only thicker because a and b effect how many times around the circle the function goes.

Notice how this function is thicker since a and b = 10 than when a and b = 1

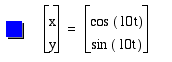
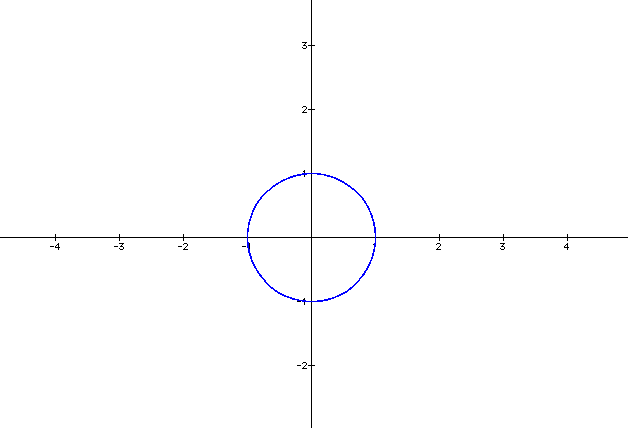
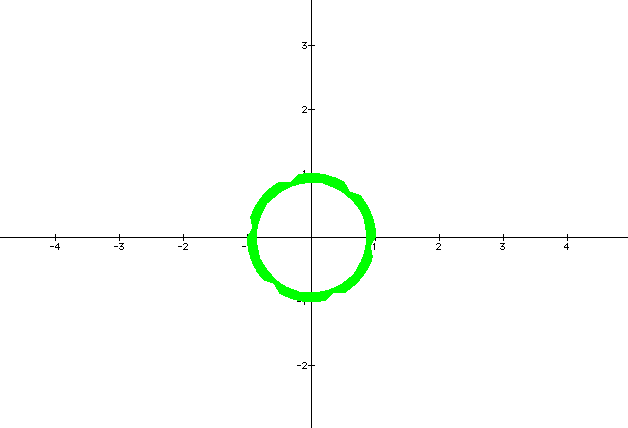
Notice how thick this is when a and b = 100. The circle is much thicker. I am not sure why there are some indentations in the circle as the curve is parameterized.

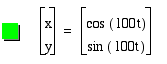
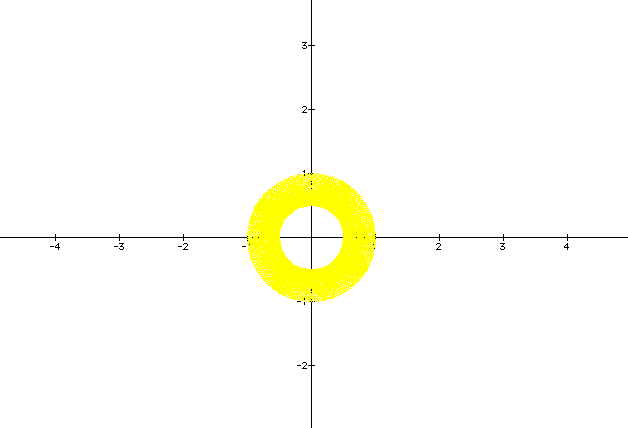
I did notice, however, that as a and b get really large, it apears that the indentations go away somewhat. However, the circle does become really thick. See the graph below when a and b = 1000. This graph is in yellow. Do you think that when a and b would be at something like 1,000,000 that the circle would be completely filled in? Let's see.

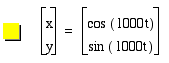
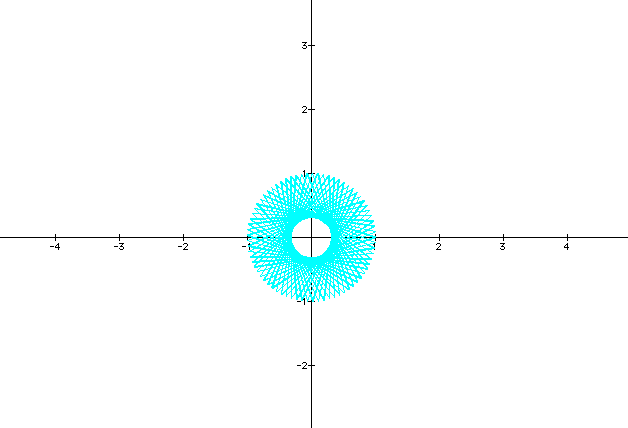
The center of the circle does become smaller as the curve parameterizes 1000000 times in the graph below. Notice the cool graph this pair of functions graphs. Notice the presence of the segments whose endpoints form the boundary of the circular curve. I found a neat website where you can go and plot any parametric curve of your choice. Click here to go to that website and do some exploring of your own. You may get a syntax error when you pull it up, but you can type in the values below to get it working!

For f, you can put in cos(t)

For g, you can put in sin(t)

Then for the parameter, type t.

For a and b, put 0 to 2*pi.

Use * for multiplying two values

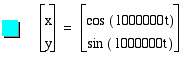
Let' s look further and see how a and b affect the parametric curve when we plug a and b into the function like below:

x= acos(t)

y= bsin(t)

Notice below when a and b are equal to 2 that the effect these values have is to increase the radius of the original circle by 2. Where x= cos(t) and y=sin(t) have a radius equal to 1, the graph of x=2cos(t) and y= 2sin(t) has a radius equal to 2.

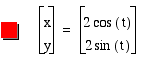
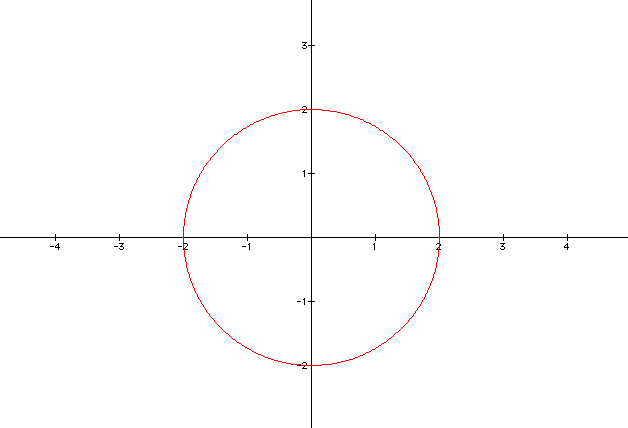
Let's try it with a and b = 5 and see it this produces a radius of 5. It does, therefore by altering a and b in this way effects the radius of the circle. I know that some of the circle is cut off but it does have a radius that goes through the points 5.

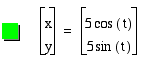
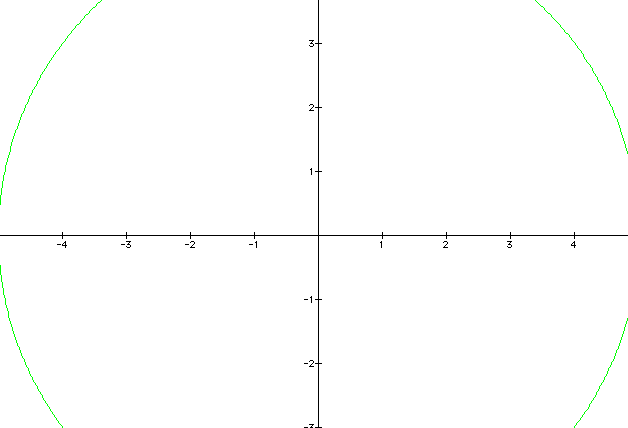
What happens when a and b are negative? Do you think the radius is the same as when a and b were positive? Let's take a look at the parametric curve when a and b = -3.

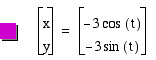
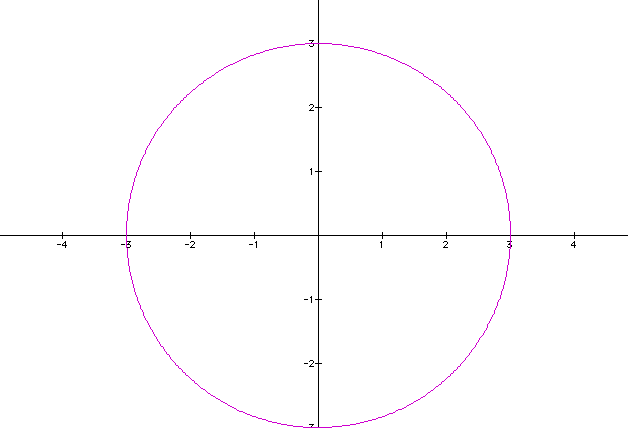
It doesn't seem that the negative has an effect on the radius of the circle. This is because the area of a circle is represented by the formula A= pir^2. Since the radius is squared, it wil always be positive which this case shows.

Let's investigate the following functions for different values of a and b, particularly when a=b, a<b, and a>b.

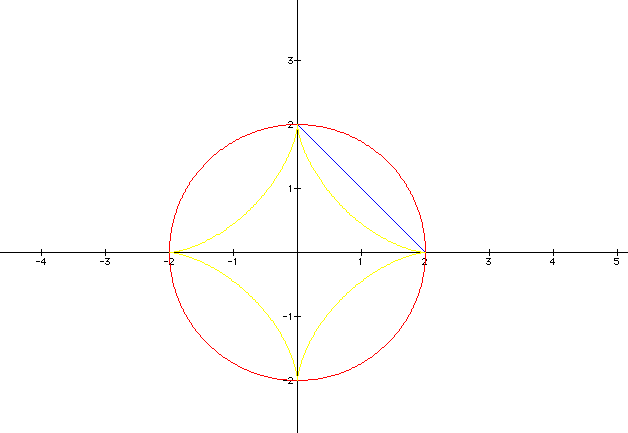
We will start off where a=b. I picked the values of a and b to be equal to 2.

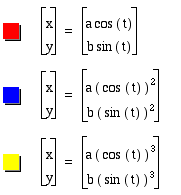
Remember, the a value corresponds along the x-axis and the b value corresponds along the y-axis.

With a and b = 2, we get to be a circle where it has a radius of 2. The blue function represents the square of the first function and the yellow function represents the cube of the first function. Notice the square function (second function) is in the first Quadrant where it is always positive. This is because anything squared is always positive. This function appears to be a segment and has endpoints at (2,0) and (0,2). Finally, the cube function looks like a diamond. It is in yellow and has points of intersection at the points (2,0),(0,2), (-2,0), and (0,-2).

Let's see what looks different when we take a>b. Let's let a=3 and b=2. See the graph below.

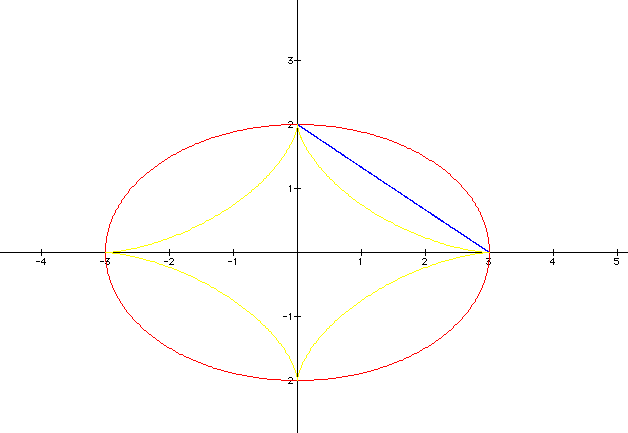
Now that a>b where 3>2, we see that for the value of a along the x-axis, the function intersects the x-axis at the points (3,0) and (-3,0). For the value of b along the y-axis, the function intersects the y-axis at the points (0,2) and (0,-2). This function appears to be an ellipse when a>b.

For the second function in blue, it still appears to be a segment and it intersects the point (0,2) along the y-axis and the point (3,0) along the x-axis. It is still in the first quadrant because all values of the function will be positive.

For the third function, the cube function in yellow, it still looks like a diamond. Its points form at the points (0,2) and (0,-2) along the y-axis for the values of b and at the points (3,0) and (-3,0) along the x-axis for the values of a.

Notice how all of the functions cross the x and y-axis at the same points.

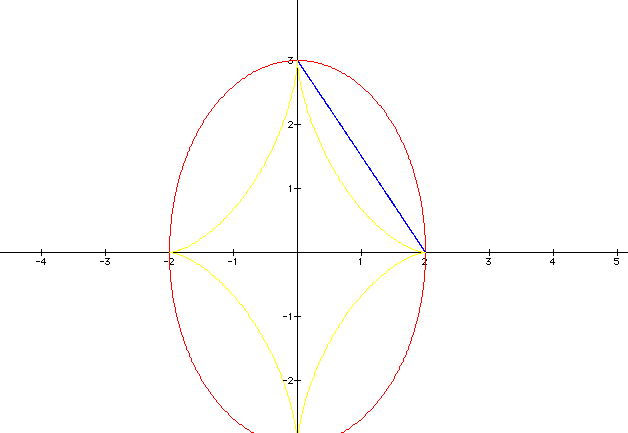
Now that a<b where 2>3, we see that for the value of a along the x-axis, the function intersects the x-axis at the points (2,0) and (-2,0). For the value of b along the y-axis, the function intersects the y-axis at the points (0,3) and (0,-3). This function appears to be an ellipse when a<b.

For the second function in blue, it still appears to be a segment and it intersects the point (0,3) along the y-axis and the point (2,0) along the x-axis. It is still in the first quadrant because all values of the function will be positive.

For the third function, the cube function in yellow, it still looks like a diamond. Its points form at the points (0,3) and (0,-3) along the y-axis for the values of b and at the points (2,0) and (-2,0) along the x-axis for the values of a.

To sum it up, if a>b, then the functions will be longer or more spread out along the x-axis. If a<b, then the functions will graph longer along the y-axis. Only when a=b, does the function form a circle. Otherwise, it forms an ellipse. All of the three functions cross the x and y-axis at the same points in all cases.

This concludes my investigation of parametric curves.

RETURN