Here is a picture of a parallelogram.
The diagonal of a parallelogram divides the parallogram into two triangles. Take a look at the picture below.
Theorem: The area of a parallelogram is equal to its base times its height.
One Way to Prove:
We will prove this using the above figure.
Let 
be a diagonal of the parallogram ABCD. The claim is that 
.
by Alternate Interior Angles with one set or parallel lines.
by
Alternate Interior Angles with the other set of parallel lines.
Then 
by
Angle Side Angle Congruence.
The area
of the whole parallelogram ABCD = 2 Area 
= 2 (1/2)(base)(height)
= (base)(height).
Therefore, the area of a parallelogram is equal to its base times its height.
A Second Way to Prove:
We can take the parallelogram ABCD and inbed it in a rectangle (AFCE). See this illustration below.
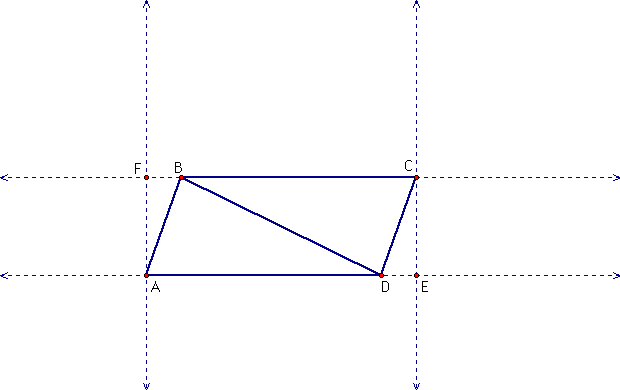
because of similar triangles.
The area
of the rectangle AFCE is equal to its length times its width or
.
Since
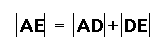, we can substitute in for the AE.
Hence,
we getArea AFCE =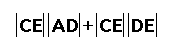 
.
The Area of the parallelogram ABCD = the (Area of the rectangle AFCE) - (the area of triangle ABF + the area of triangle CDE).
Therefore,
the Area of ABCD =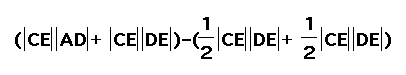
= 
= 
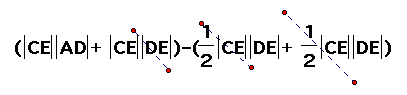
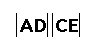or
the parallelograms base times its height.
Therefore, we have proved a second way that the area of a parallelogram is equal to its base times its height.