Using the figure below, we will prove the Sine and Cosine Addition formulas for the two angles x and y.

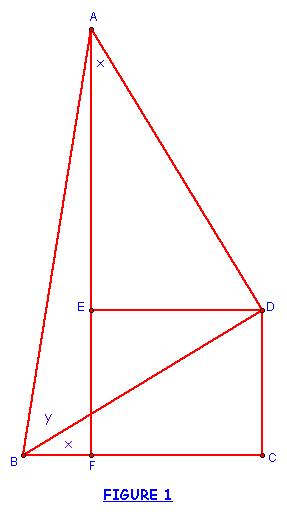
Note that are all right triangles.

The sine addition formula states that

sin(x+y) = cos(x)sin(y) + sin(x)cos(y).

Let's see if we can prove this is true using the above Figure 1.

sin(x+y) = .

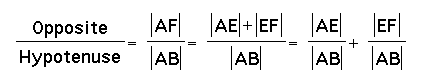Since EDCF is a square, then segment EF is congruent to segment DC so...

sin (x+y) = .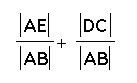

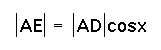and 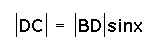, then

sin(x+y) = .

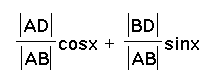Finally, since 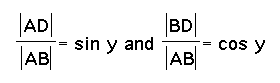, we are left with sin(x+y) = siny cosx + cosy sinx.

Therefore, we have proved the sine addition formula does work!

Note again that are all right triangles.

The cosine addition formula states that

cos(x+y) = cos(x)cos(y) - sin(x)sin(y).

cos(x+y) = .

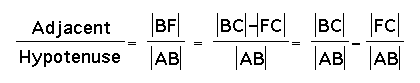Again, since EDCF is a square, then segment FC is congruent to segment ED, so substiting in for this, we get

cos(x+y) = .

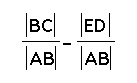Since 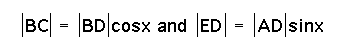, we get

cos(x+y) = .

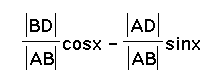And since 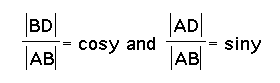, we are left with

cos(x+y) = cosycosx - sinysinx.

We have proved how the sine and cosine addition formulas work!

RETURN