

Let's review what the orthocenter of a triangle is before beginning this investigation.
The orthocenter of a triangle is the common intersection of the three lines containing the altitudes. An altitude is a perpendicular segment from a vertex to the line of the opposite side.
Okay, now we
can begin!
Let's construct a triangle ABC and construct the orthocenter H of this triangle ABC.
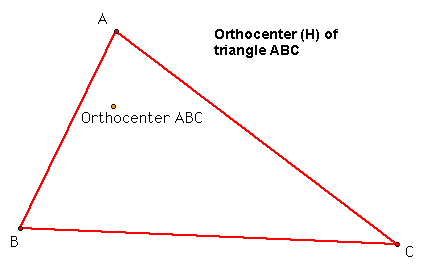
Construct the orthocenters of triangles HBC, HAB, and HAC. These are given below.
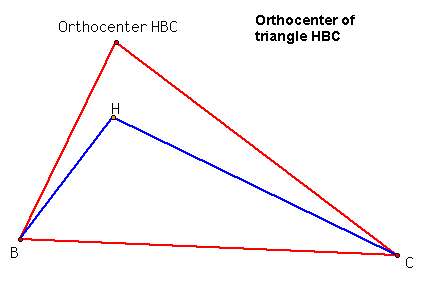
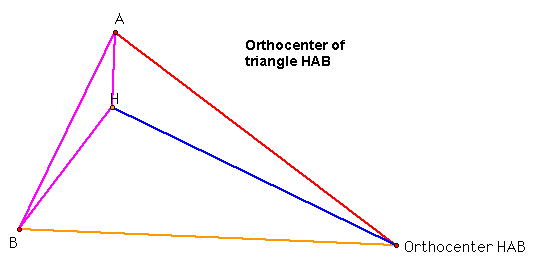
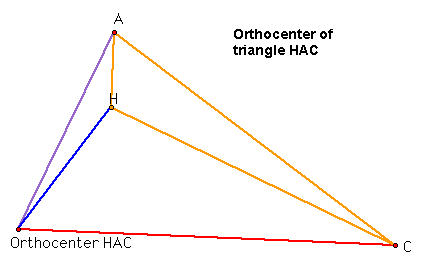
Something interesting appears to me. Well, for one, the orthocenter of triangle ABC, H, is one of the vertices for each of the other three triangles. It seems that the orthocenters of all the three small triangles HBC, HAB, and HAC fall on one of the vertices of the original triangle ABC.
For the triangle HBC, the orthocenter is on the point A. Notice how the point A isn't one of the vertices on this triangle.
For the triangle HAB, the orthocenter is on the point C. Notice again how the point C isn't one of the vertices on this triangle.
Finally, for triangle HAC, the orthocenter is on the point B. Once again, notice how the point B isn't one of the vertices on this triangle.
This is an interesting observation. It appears that the orthocenters of the three smaller triangles contained in the larger triangle have their orthocenters on a vertex of the large triangle that isn't contained in the small triangle of interest. That is pretty neat!
Okay, now let's take a look at the circumcenter. The circumcenter is the point in the plane equidistant from the three vertices of the triangle. To find the circumcenter, you take the perpendicular bisector of each segment in the triangle.
The circumcenter is the center of the circumcircle.
Let's now construct the circumcircle of triangle ABC. See the graph below.
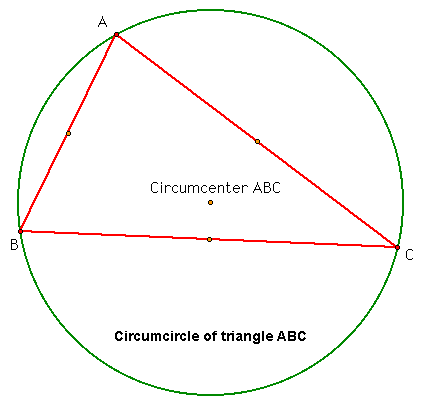

Notice how the definition of a circumcenter holds for triangle ABC. It is the point that is equidistant from the three vertices of the triangle. All of these three distances are shown to be the same above.
Let's also look at the circumcircles for the triangles HBC, HAB, and HAC. See these below.
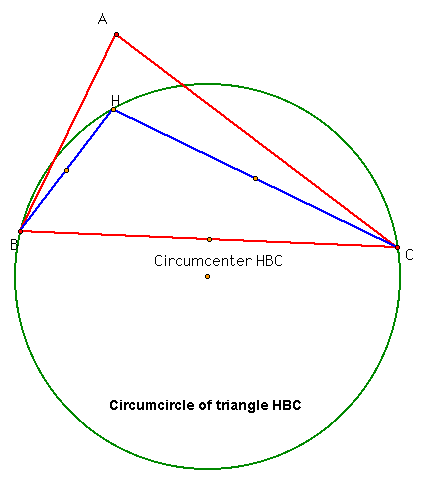


Notice here how the distances are also the same from the circumcenter to the vertices of the triangle HBC. Also, notice how the circumcenter lies closest to the line segment BC instead of HB or HC where H is the orthocenter of the triangle.
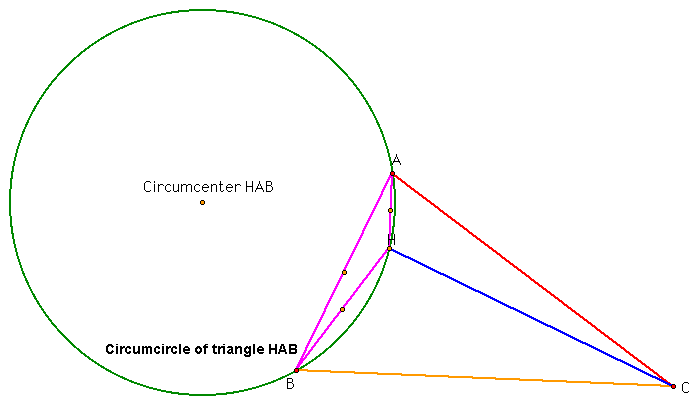


The same observation can be made here. The circumcenter does lie equidistant from the vertices of the triangle HAB. Also, the circumcenter lies closest to the segment AB and not the segments HA and HB.
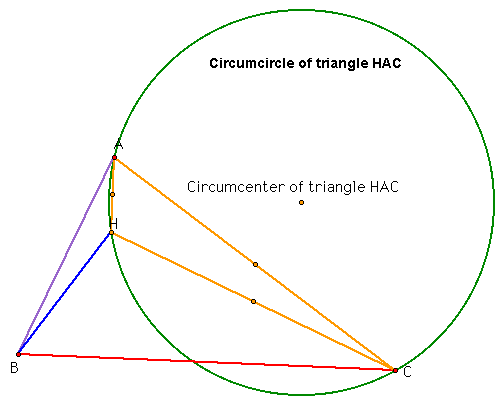


Finally, for the triangle HAC, the definition of the circumcenter holds because the vertices of the triangle HAC are equidistant from the circumcenter. In addition, the circumcenter lies closest to the segment AC instead of the segments HA and HC which both contain the orthocenter of the triangle (H).
Since it is hard to tell how all the circumcenters and circumcircles relate when separated, I did a separate construction and put them all together to see how they relate. See the graph below.
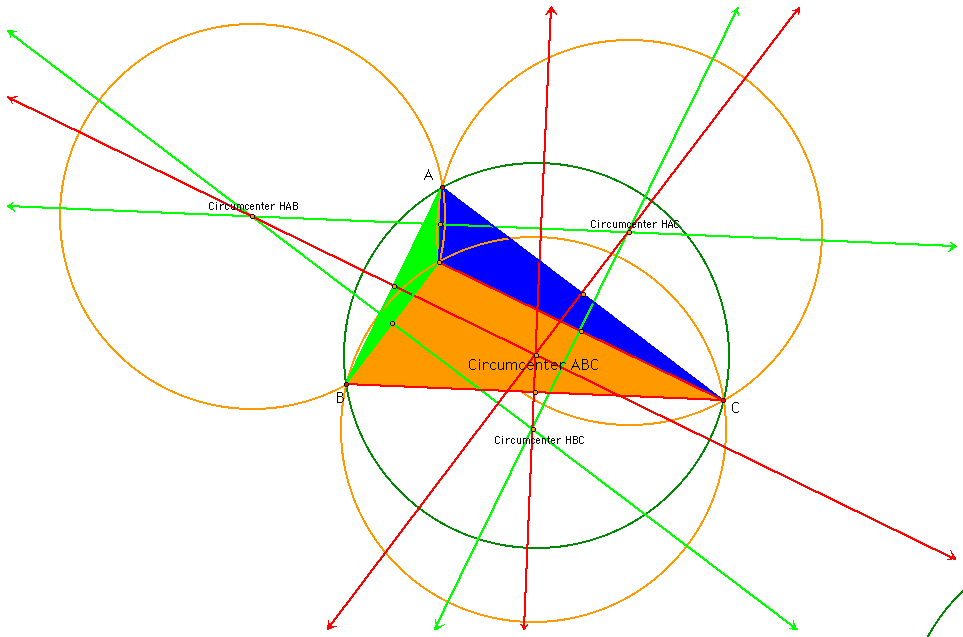
Okay, let's explore the results when we look at the circumcenters and circumcircles for all four triangles. I see a really cool relationship. Do you notice how the perpendicular lines that come together to form each circumcenter go through the circumcenters for the other three triangles.
Let's take for instance the triangle ABC. Its circumcenter is formed at the intersection of the three red perpendicular lines in the above graph. Let's first look at the perpendicular lines that bisects the segment BC. Do you notice that this line goes through the orthocenter of the triangle HBC?? Notice the connection with the segment BC and the orthocenter of HBC.
Now, let's look at the perpendicular line that bisects the segment AC. I don't think it is a coincidence that it goes through the orthocenter of the triangle HAC. Notice again the connection with line segment AC and the orthocenter of HAC.
Finally, let's take a look at the perpendicular line that bisects the segment AB. This line goes through the orthocenter of triangle HAB. Once again, there is a connection with line segment AB and the orthocenter of HAB.
That is really neat. The same holds true when you look at the other triangles. Do some exploration on your own to see if I am right!
This concludes my exploration of altitudes and orthocenters.