What is a pedal triangle?
Given a point P which can be any point in the plane and any triangle, the pedal triangle of P is the triangle whose vertices are the feet of the perpendiculars from P to the side lines.
Click here to go to Math World's website and learn more about pedal triangles.
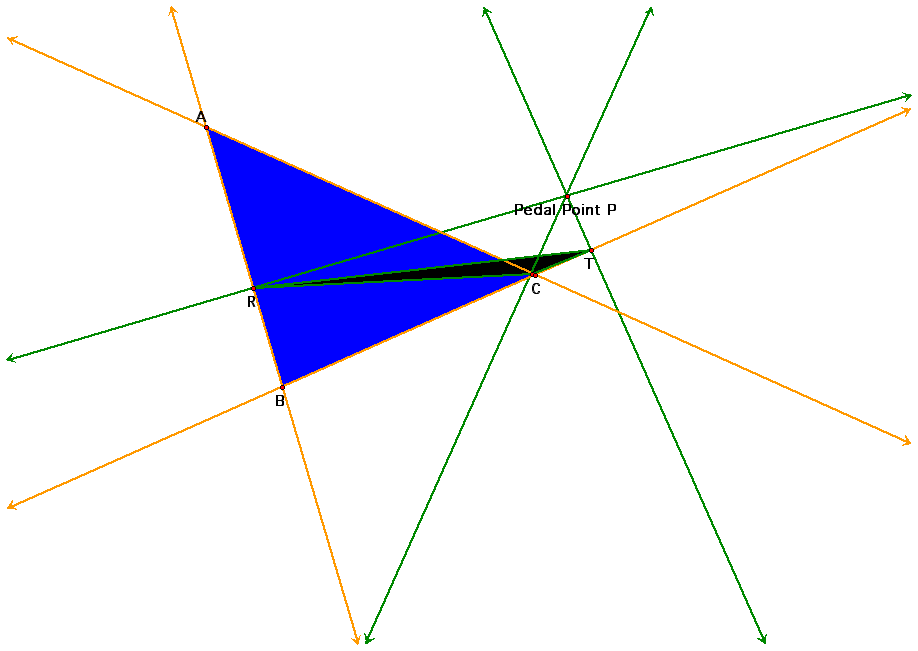
Let's do a construction of a pedal triangle. First, I am going to take a triangle ABC and pick any point P in the plane. Then, I will construct the perpendicular lines through the point P to each side of the triangle ABC.
Notice the triangle in blue is the triangle ABC and the triangle in black in the triangle RST which is the pedal triangle for the pedal point P.
The yellow lines form the sides of the triangle ABC and the green lines are the perpendicular lines that go through the pedal point P to each side of the triangle ABC.
Click here to for a script tool
of the pedal triangle above where you can play around with the
triangle.
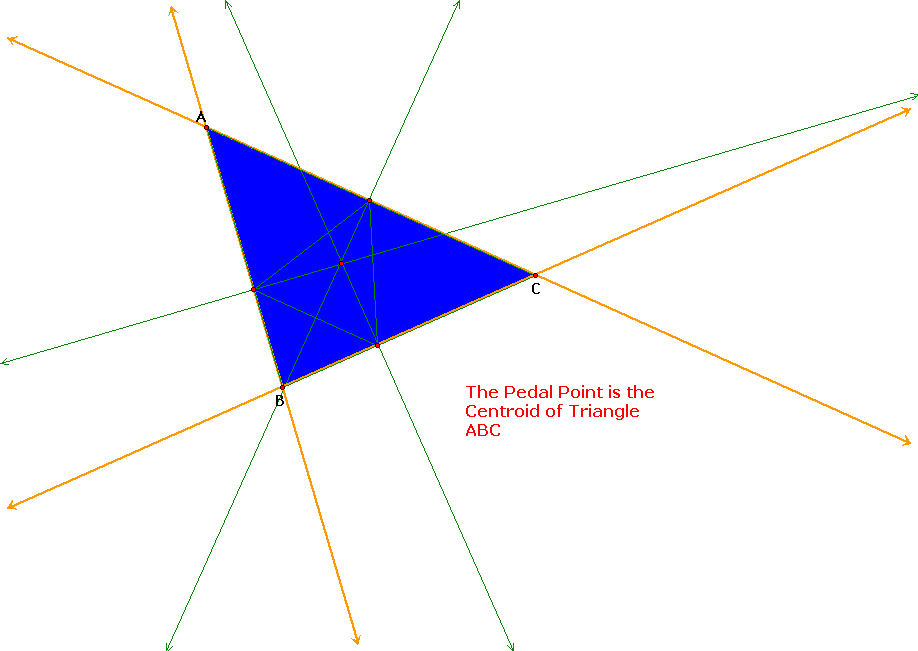
Notice how the pedal triangle is located all the way inside the triangle ABC when the pedal point P is the centroid of the triangle ABC.
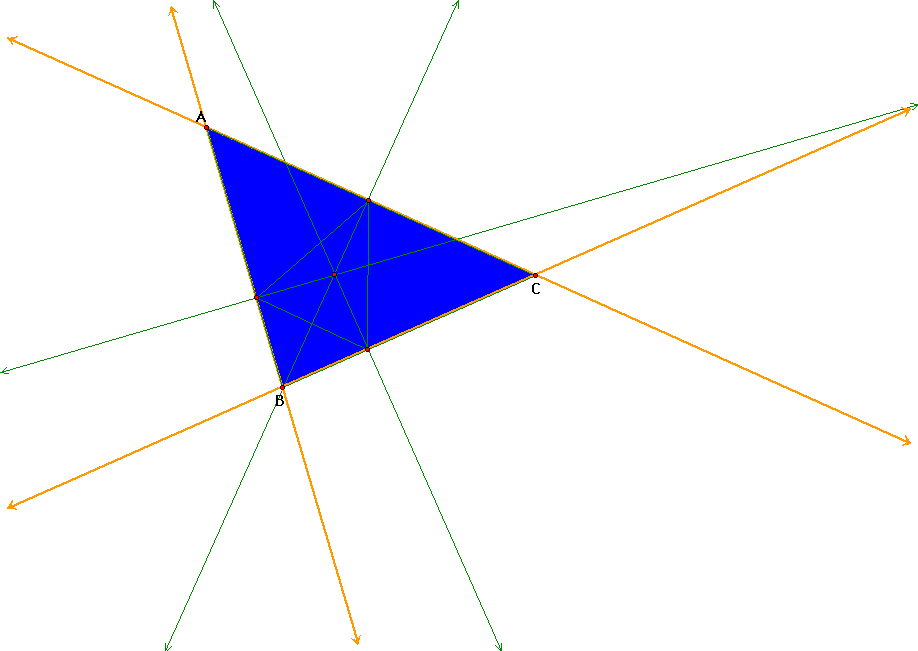
Notice, now that the pedal triangle is located once again inside the triangle ABC when the pedal point P is the incenter of triangle ABC. The pedal triangles when P is the centroid and the incenter do look almost the same.
Let's look at the pedal triangle when the pedal point P is the orthocenter of triangle ABC.
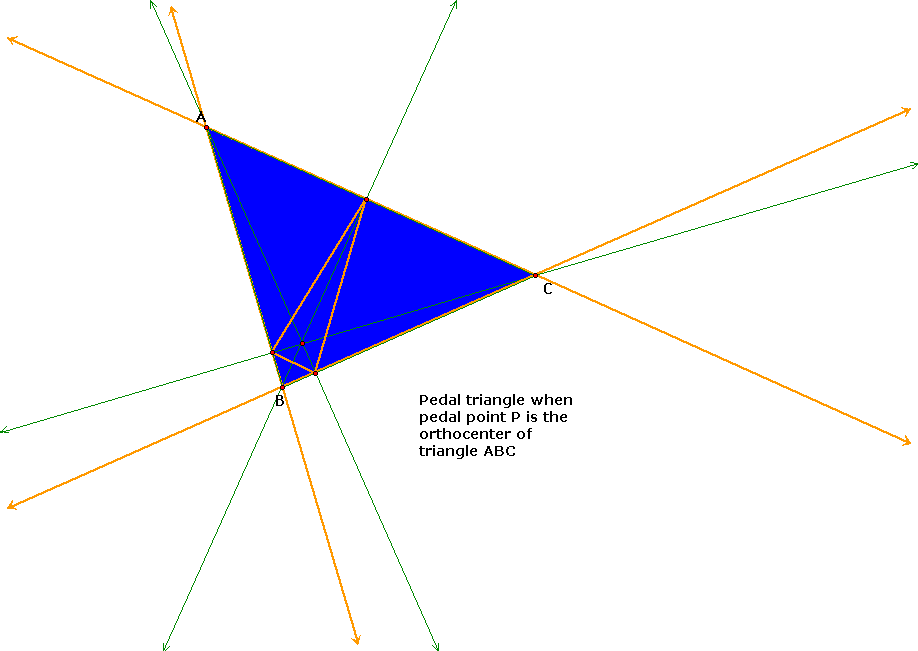
Here is an interesting observation. When the pedal point is the orthocenter of triangle, the pedal triangle and the orthic triangle are one and the same. This makes sense when you recall the definition of the orthocenter. It is the common intersection of the three lines containing the altitudes. An altitude is just a perpendicular segment from a vertex to the line of the opposite side. Remember, the definition of a pedal triangle is one whose vertices are the feet of the perpendiculars from P to the side lines. These definitions form the same triangle when P and the orthocenter are the same points.
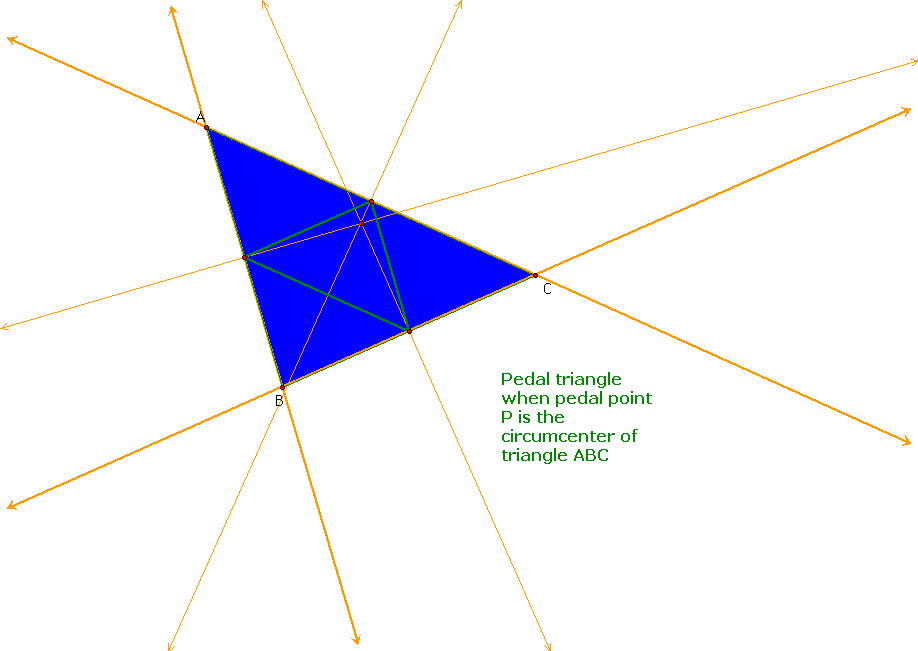
Now, let's see what the pedal triangle looks like when P is the Circumcenter of the triangle ABC. Here, since P is the circumcenter, it is the center of the Circumcircle or the circumscribed circle of the triangle.
Notice how the vertices of the pedal triangle lie at exactly the point of intersection where the perpendicular lines that form the circumcenter intersect each side of the triangle.
This is because the circumcenter is found by the intersection of the perpendicular bisectors of a triangle.
What happens to the pedal triangle when the pedal point P is on one of the sides of the triangle ABC?
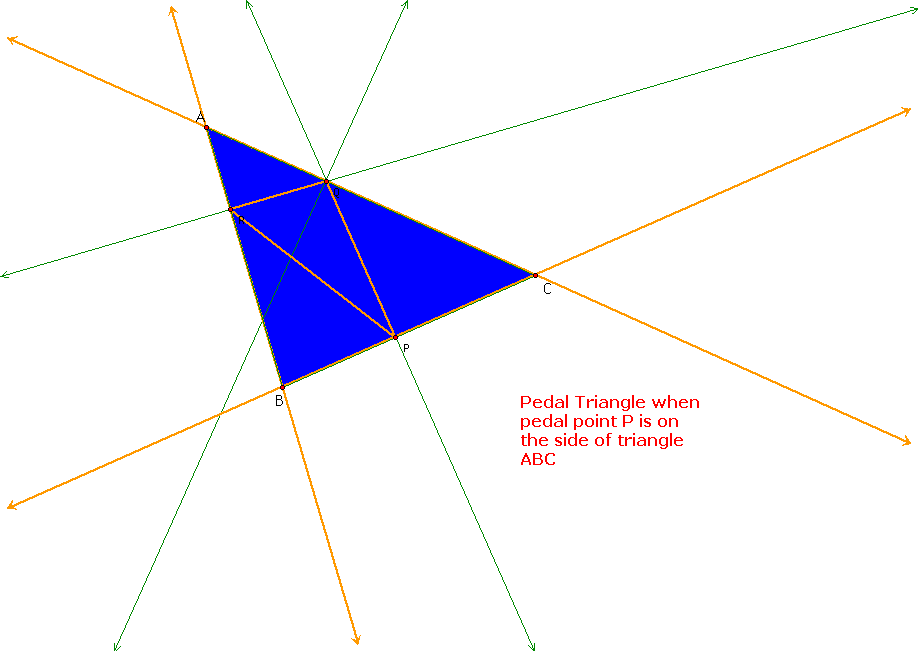
The pedal triangle still lies inside the triangle ABC as in all the cases I have explored so far. Here, the pedal point P serves as one of the pedal triangle vertices as well. This is the first time this case has happened thus far.
Now, let's look at the pedal triangle when P is on one of the vertices of triangle ABC. Or, is there a pedal triangle in this case?
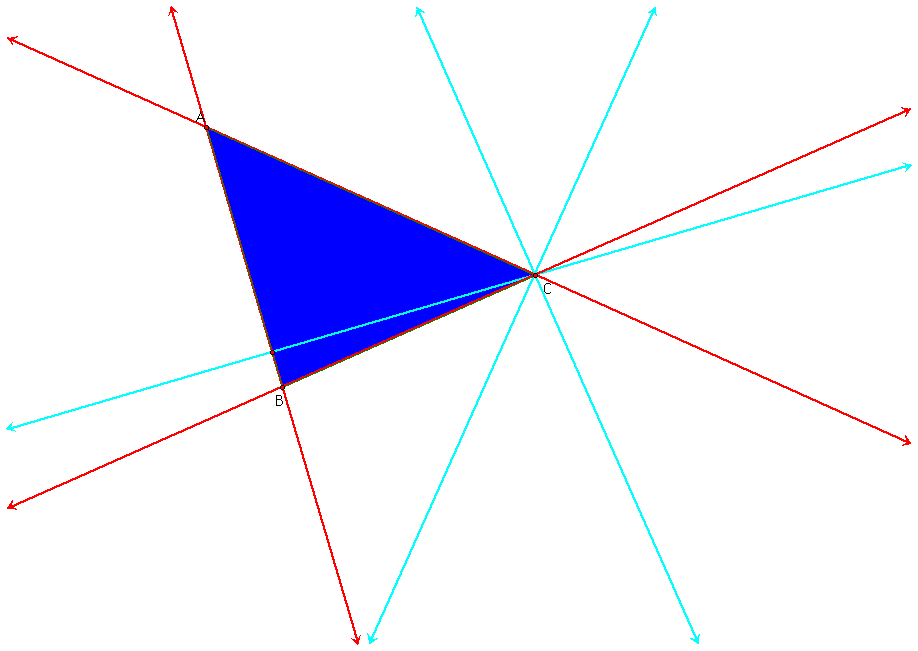
There isn't a pedal triangle in this case because two of the perpendicular lines (shown in light blue above) to the sides of the triangle go through the same point. Therefore, you only have two points to construct a triangle with and that can't happen!
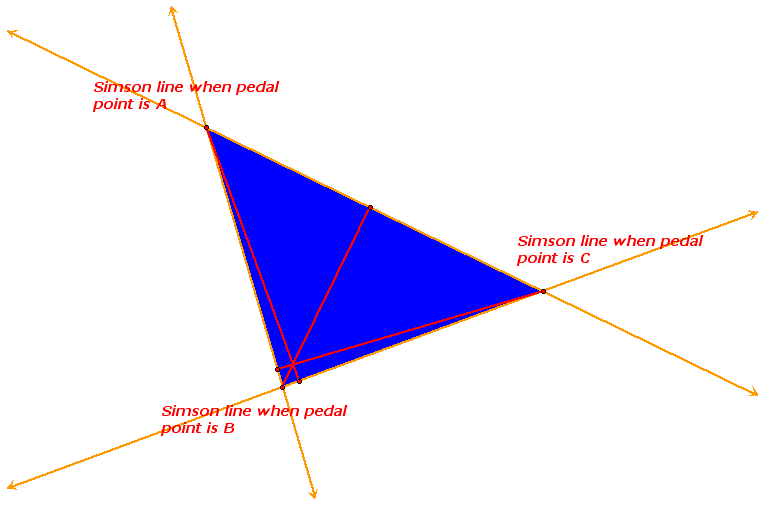
The vertices of the pedal triangle are colinear and form a degenerate triangle when the pedal point lies on one of the vertices of the triangle that you started with which was ABC in this case. This scenario was just discussed when I tried to construct a pedal triangle when the pedal point was one of the vertices of the triangle ABC. I placed the pedal point on the vertex C and there wasn't a pedal triangle formed because all of the three vertices of the pedal triangle were colinear. Two of them were the same point, C and the other one was the point where the pedal point P perpendicularly intersected the line segment AB.
The line segment formed upon connecting the vertices of the pedal triangle when all three of the vertices of the pedal triangle are colinear is known as the SIMSON LINE.
See the construction below of three Simson lines when the pedal point P is on each of the triangle ABC's vertices.