

A. Consider any triangle ABC. Select a point P inside the triangle and draw lines AP, BP, and CP extended to their intersections with the opposite sides in points D,E, and F, respectively.
Explore (AF)(BD)(EC) and (FB)(DC)(EA) for various triangles and various locations of P.
B. Conjecture? Prove it. Consider the ratio
C. Show that when P is inside triangle ABC, the ratio of the areas of triangle ABC and triangle DEF is always greater than or equal to 4. When is it equal to 4?
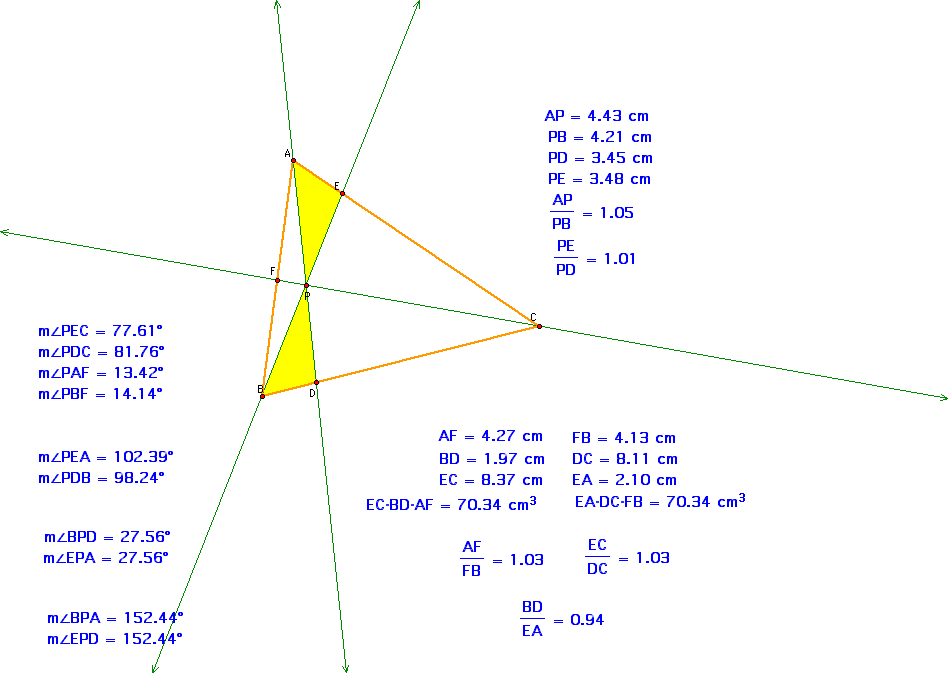
Exploration of (AF)(BD)(EC) and (FB)(DC)(EA) for this triangle ABC. Notice how the product of each of these three segments is equal to 70.34 cm^2.

I decided to take a variety of measurements of the triangles and sides of this particular triangle ABC.
I found that the ratio of AF to FB = 1.03 and the ratio of EC to DC = 1.03. I also found that the angles BPA and EPD have the same angle of 152.44 degrees. Also, the angles BPD and EPA have the same angle measurement of 27.56 degrees. These angles are alternate interior angles.
This would make sense since the angles BPA and BPD add up to form 180 degrees. Does 152.44 + 27.56 = 180? Yes! This is the same case for the angles EPD and EPA. These two angles add up to form a straight line having an angle of 180 degrees.
Let' s look at another triangle and make the same comparisons when the point P is inside the triangle. Click here to explore the location of P of this triangle as GSP will calculate the values I have retrieved below for different places of P. Notice that as you move P around the the inside of triangle ABC, the relationship between the areas of the triangle ABC and triangle DEF are always greater than or equal to 4.
Notice how again, for this triangle we get the same relationship where
is equal to 1. If we take 101.18/ 101.18, we get a ratio of 1 between the two.
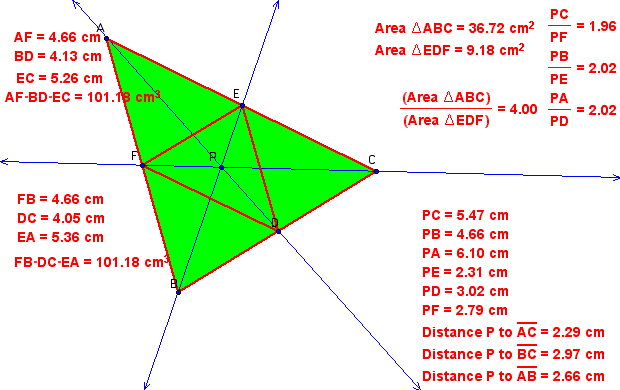
Below, I constructed the centroid of the triangle ABC where the three medians of the triangle ABC intersect. I compared this point to the point P when the ratio of the area of triangle ABC to triangle DEF is 4. It appears that these points are almost the same point.
Now, for the proof that the ratio of
(AF)(BD)(CE)
(BF)(CD)(AE)
is always equal to 1.
We begin with the triangle ABC and P any point inside of this triangle.
I constructed a parallal line through the point A to the line BC. Here is what this lookw like>
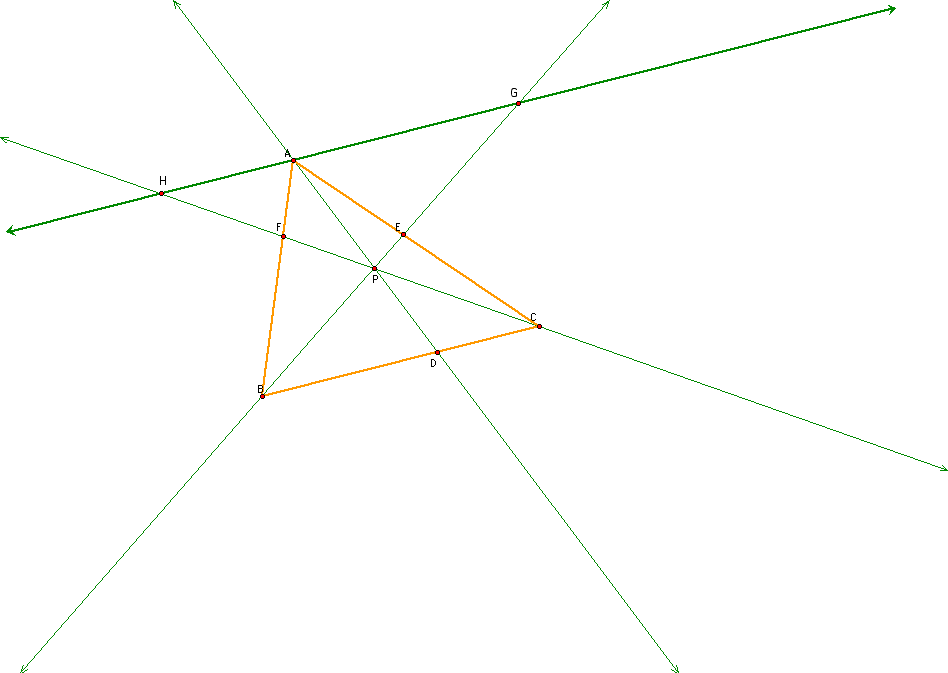
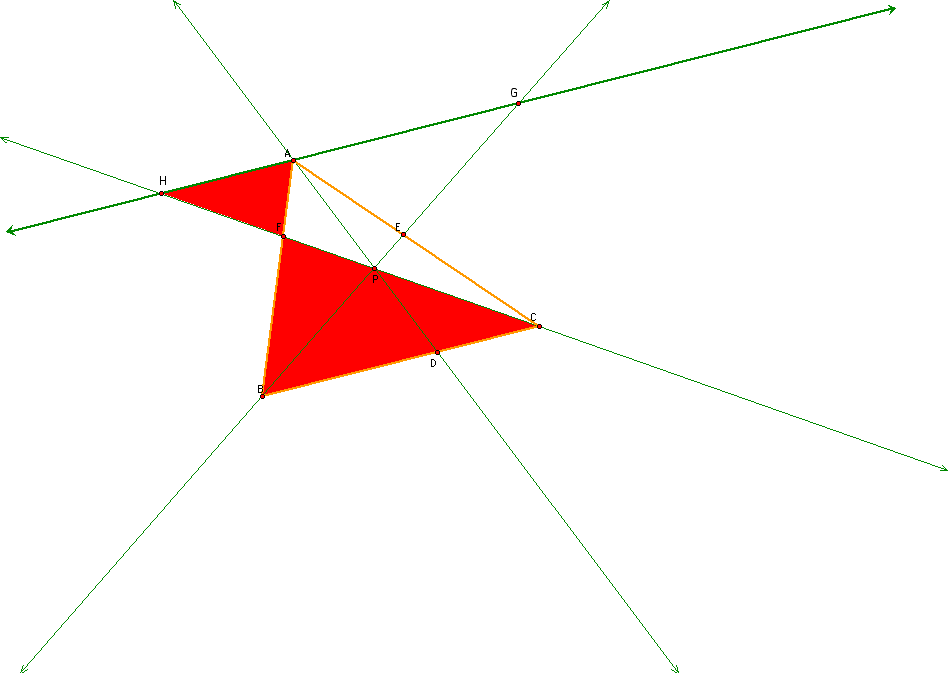
Next, I see that the triangles FAH and FBC are similar triangles such that
The triangles EGA and ECB are also similar triangles such that
AG/ BC = AE / EC = GE / EB. See this illustration below.
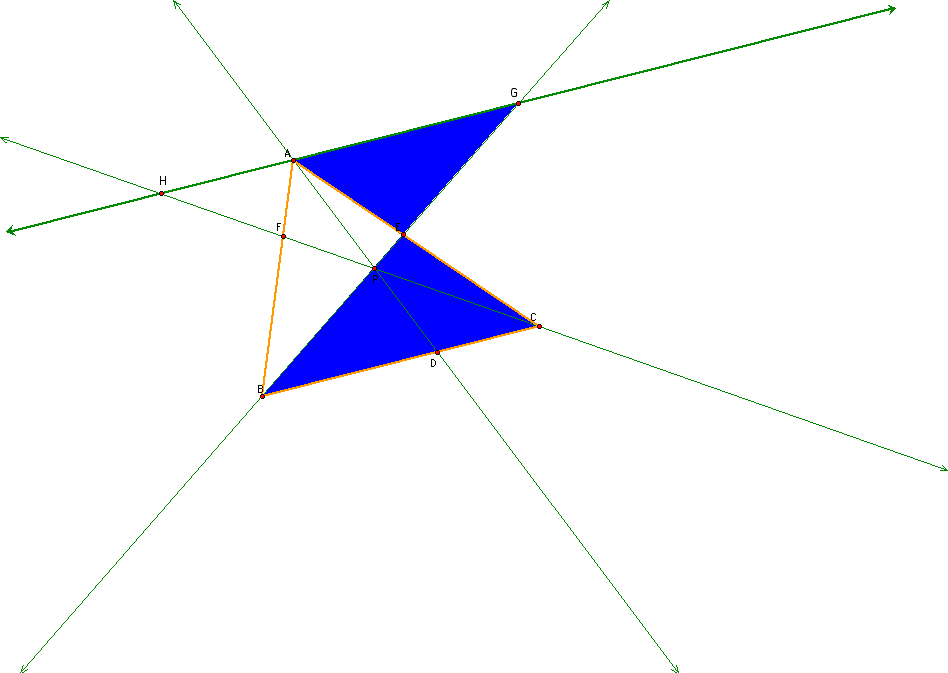
Triangles AGP and DBP are also similar triangles where AG/BD = AP/DP = GP/DP
See the graph below for these triangles.
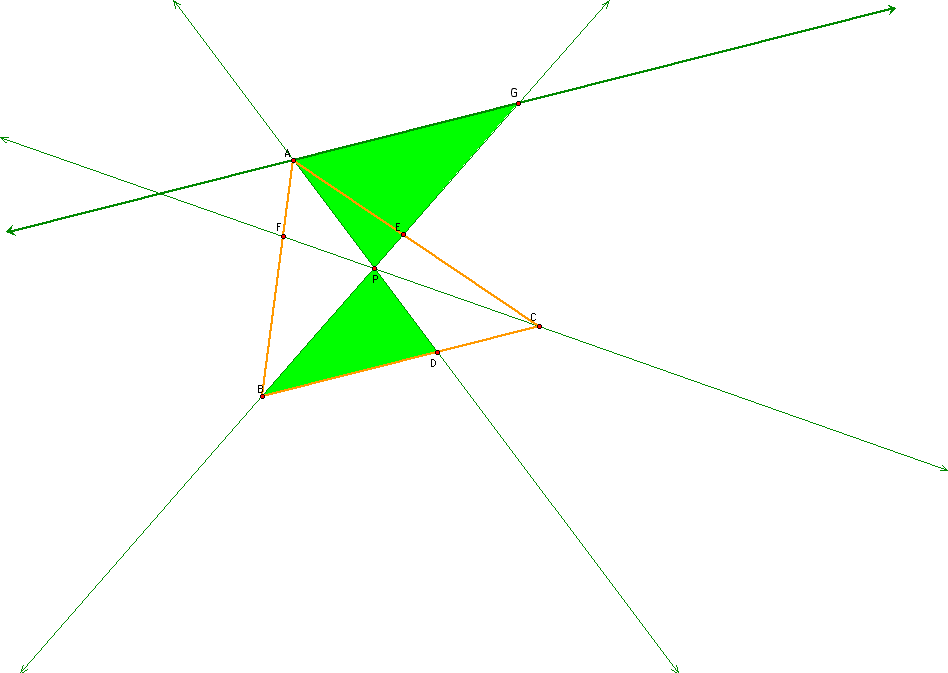
Finally, triangles CDP and HAP are similar where the sides form a ratio where
HA/ DC = AP/ DP = HP/ CP.
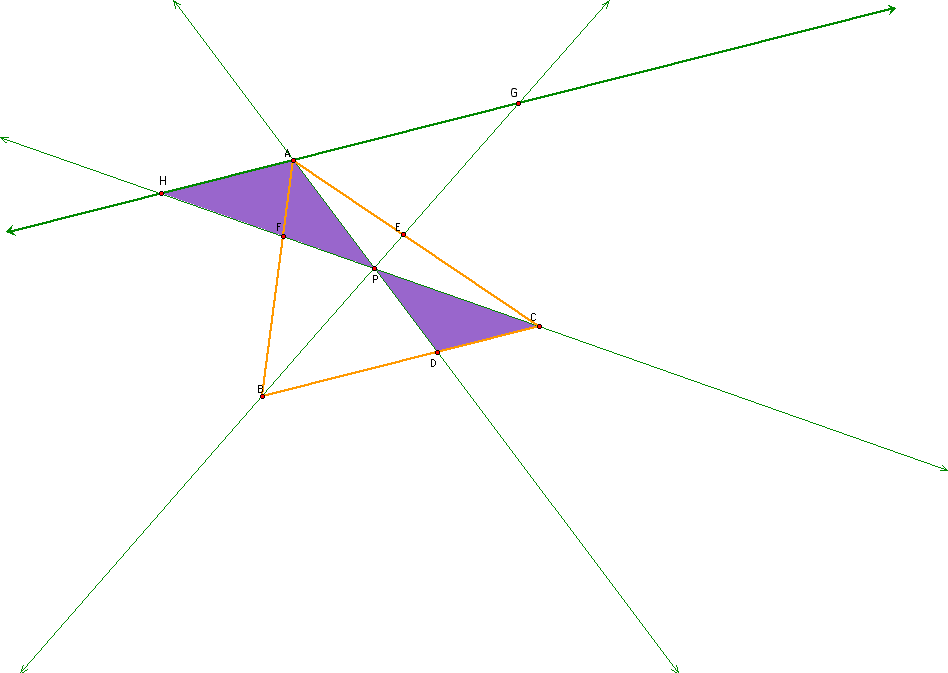
Notice how HA/ DC = AP/ DP and AG/BD = AP/ DP.
Therefore, HA/ DC = AG/ BD and BD/ DC = AG/ AH by cross-multiplying.
From above, we can conclude by saying
HA/ BC = AF/ BF
CE/ EA = BC/ GA
BD/ DC = AG/ AH (what we just found)
Multiplying these gives us
(HA/BC)(CE/EA)(BD/DC) = (AF/BF)(BC/GA)(AG/AH)
This simplifies to 1 and proves that the ratio of
(AF)(BD)(CE)
(BF)(CD)(AE)
is always equal to 1.
This concludes my investigation of the problem for the final assignment.