

We will begin reviewing today about what we covered yesterday.
When writing two triangles are congruent, what matters?
ORDER MATTERS
As a class, we will go over some examples together regarding overlapping congruent triangles. We will practice picking out the line of symmetry for the figures (if there is one). We will work on labeling the triangles congruent in the proper order.
Next, I will lead into the discovery of the Angle-Angle-Side Congruence Theorem.
I will lead in to the topic of discussion by drawing two triangles on the board and label that two angles and a non-included side are congruent in each triangle. I will ask the students if they think the triangles are congruent based on what is given.
These triangles are, in fact, congruent. By what new theorem do you think they are congruent?
We have two angles and a non-included side congruent to two angles and a corresponding non-included side.
So, by Angle-Angle-Side Congruence, the triangles are congruent.
I will write the theorem on the overhead for them to copy down.
Theorem: Angle-Angle-Side Congruence Theorem
If two angles and a non-included side in one triangle are congruent to two angles and the corresponding non-included side in another triangle, then the triangles are congruent.
Then we will do this two-column proof of why the Theorem works.
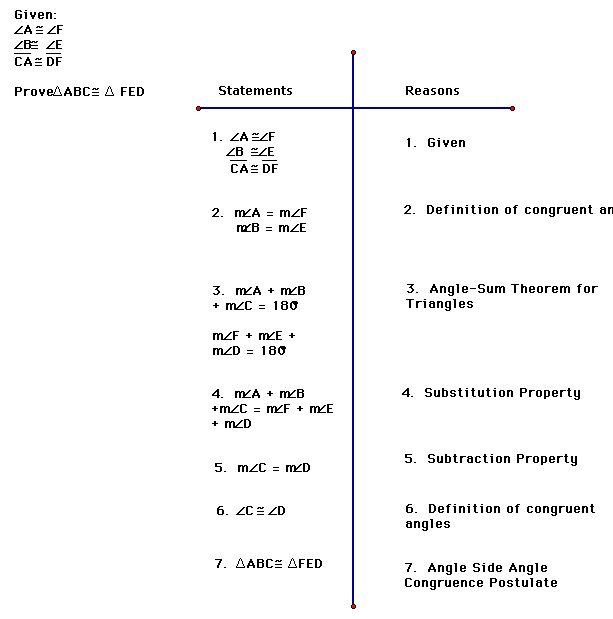
So what does this tell you about Angle-Angle-Side Congruence? It works because since you have two corresponding angles congruent in the triangles, you can find the third angle measurement and use Angle-Side-Angle Congruence. THIS IS BECAUSE THE THREE ANGLES IN A TRIANGLE SUM TO 180 DEGREES.
We will work through some examples in the section to practice using the Angle-Angle-Side Congruence Theorem. The examples involved will include the use of parallegrams and how alternate interior angles are congruent. I will give them an example where two triangles are inscribed in a square and they have to use what they know about the sides of the square to prove the triangles congruent. I will make sure to do some previous examples involving other congruence theorems or postulates to see if they can distinguish between when to use each one.
I will close with a review of the Angle Angle Side Congruence Theorem and assign a couple of problems involving this theorem from the book. I will tell them how tomorrow we are going to look at a special case for proving right triangles congruent with the Hypotenuse Leg Theorem.