
Janet Kaplan
The Cycloid A
Parametric Function
Some curves are most conveniently
represented by two functions, both of which use the same parameter. The trigonometric
functions Sine (t) and Cosine (t), for instance, are both functions of a
specific angle, t.† We call the pair
Parametric Equations.† When graphing
parametric equations on the Cartesian plane, each point (x,y) represents the
value of two individual functions, one represented by the x coordinate and the
other represented by the y coordinate.
An easily recognized example of a parametric representation of a curve is that of a circle of radius 1 centered at the origin. We have the relationships between a point (x,y) on the circle and an angle t as shown in the following figure.
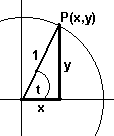
By elementary trigonometry we have the parametric equations
x = cos(t), y = sin(t).
As t goes
from 0 to 2p the corresponding points trace out the circle in a
counter clockwise direction.
The Cycloid:
Based upon the parametric function of a
circle, the Cycloid is a most
interesting and famous curve.† It
received its name from Galileo in 1599.
Picture the journey an ant would have
clinging to a spot on a bicycle wheel which is riding down the street.† Or how about a cow paddy (buffalo chip)
smashed into the perimeter of a covered wagon wheel?† What path would it take?† In fact, the trip would trace the form of a
cycloid.†
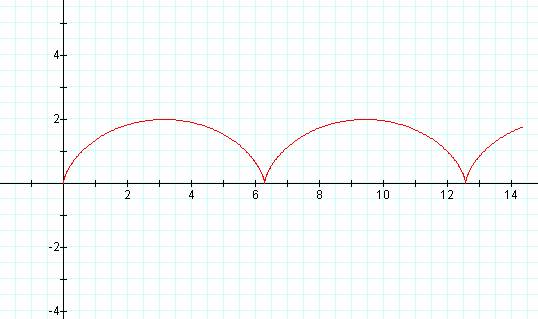
A cycloid is the path generated by a point
on the circumference of a circle as the circle rolls (without slipping) along a
straight line. Algebraically, it is the locus of a point from the center of a circle
of radius a, that rolls along a straight line.†
For each point (x,y) of the antís journey,
x = a(t
- sin(t)), y = a(1 - cos(t))
where parameter t is the angle
through which the circle was rolled. As in the case of the circle, these
parametric equations can be derived using elementary trigonometry. To see the
basics of the derivation click on the following: The equations of a Cycloid.
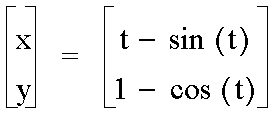
Click here for a GSP animation of the Cycloid.
RETURN
to Janet Web Page