Janet Kaplan

Conic Sections

Graphs of the form x² + nxy + y² are called Conic Sections. They include circles, ellipses and hyperbolas.

For this investigation we will vary the coefficient of the xy term, n, and explore what results we get.

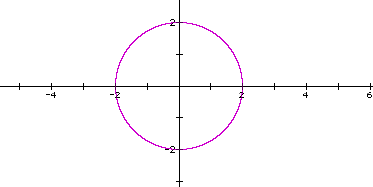
We start out with the basic equation of a circle, say x² + y² = 4. We then add a central term, xy, and examine the results as we vary its coefficient.

What will happen if we add the central term, xy? Let's set n = 1 and see what happens.

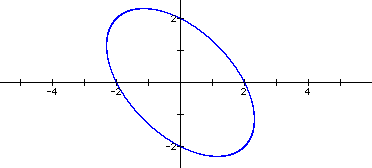x² + xy + y²

How about if we set n equal to -1? So, x² - xy + y² = 4:

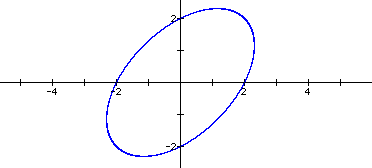
Adding that central term changes the circle into an ellipse (assuming, of course, that n does not equal 0).

But now to really see the changes taking place with our basic circle, click here. This will animate the function as n changes from -3 to 3.

_______________________________________________________________________________________________

What do you notice? First of all, the sign of n seems to determine the orientation of the ellipse. When xy has a positive coefficient, an ellipse that schews to the left is formed; when the coefficient is negative, the ellipse schews to the right.

Staying with positive coefficients for the moment, as we increase from n = 1 to 2, the ellipse elongates. This happens gradually at first, but by n = 1.8, the ellipse is very long, and at n = 2, the ellipse becomes two parallel lines!

Immediately beyond the parallel and continuing further towards n = 3, the function becomes a hyperbola. With increasing n values, the angle of the hyperbola becomes steeper.

Notice that all the while the function contains the points (2,0), (-2,0), (0,2), (0,-2).

This is perhaps the only thing that is immediately clear. What is happening to our simple circle to make it become an ellipse, then parallel lines, and then a hyperbola?

________________________________________________________________________________________________

Let’s refer to the geometry of Conic Sections to help us visualize what is happening.

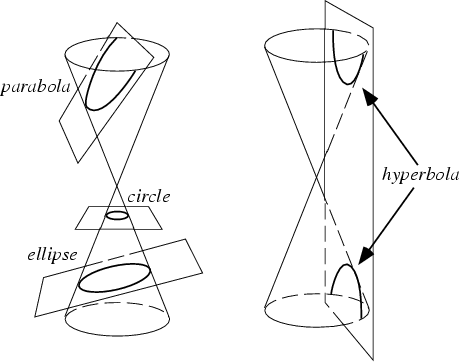
Conic sections are defined to be the nondegenerate curves generated by the intersections of a plane with one or two nappes of a cone. For a plane perpendicular to the axis of the cone, a circle is produced. For a plane which is not perpendicular to the axis and which intersects only a single nappe, the curve produced is either an ellipse or a parabola. The curve produced by a plane intersecting both nappes is a hyperbola. **

** Mathworld.Wolfram.com

The graphs above are actually a cross-section of the cone generated by the intersection of the plane. Notice how a circle is created when the plane is perpendicular to the axis of the cone. This occurs when n = 0, resulting in the equation

x² + y² = 4.

__________________________________________________________________________________________________

As n increases from 0 to 2, the circle begins to elongate into an ellipse. The plane intersecting the cone meets it at an angle, thereby creating the ellipse. The closer to zero n is, the closer the perpendicularity of the angle, and the smaller the eccentricity of the ellipse. At n = 1 the angle of the plane is somewhat steep, and the eccentricity is 0.816 (0 < eccentricity < 1). The ellipse continues to elongate as n increases towards 2, and at the exact moment that it reaches 2, the ellipse becomes two parallel lines! It is known as a degenerate curve at this point.

Again, using the three-dimensional figures above as a model, we can see how this happens. Two parallel lines occur when the plane's angle of intersection is such that it is tangent to the left surface of one nappe and to the right surface of the other nappe. It would be going through the center point of the inverted cones. Can you picture it?

Continuing the plane's ascent to an angle that is parallel to the cone's axis and perpendicular to the base, we can see that hyperbolas are formed. The hyperbola starts out quite flat when n is just slightly larger than 2, but becomes increasingly curved as it moves towards and then beyond 3 and 4.

See it? At n values just over 2, the parallel plane intersects the cone close to the center. As n increases, the plane moves outward towards the edges of the cone, bringing the eccentricity of the hyperbola down closer to one.

_____________________________________________________________________________________________________________

RETURN to Janet’s Home page