
Janet Kaplan
Construction of the
_____________________________________________________________________________
Although not actually receiving its present day name until 1842, the Nine-Point Circle was first discovered
in the early 1800s. Several mathematicians through the years have made
discoveries concerning the Nine-Point Circle, but the primary credit is given
to Euler and Feuerbach. As such, the Circle also bears their names.
The Nine-Point Circle is constructed by the composition of three sets of
significant points of a triangle. These sets are a) the midpoints of the sides
of the triangle, b) the feet of the altitudes drawn to the sides, and c) the
midpoints of the segments from the respective vertices to the Orthocenter of
the triangle (also known as Euler Points).
The Nine-Point Center U lies on the Euler Line of the triangle – the
line passing through the orthocenter H, the circumcenter O, and the centroid G
of the triangle.
This famous Circle shows up in many important theorems, one of which is
Feuerbach’s theorem. It states that the Nine-Point Circle is tangent to the
incircle of a triangle and to its three excircles, which are the circles
outside of the triangle that are tangent to the three sides.
Here we will construct the Nine-Point Circle, demonstrating how all nine
points lie on this very interesting Circle.
________________________________________________________________________________________________________
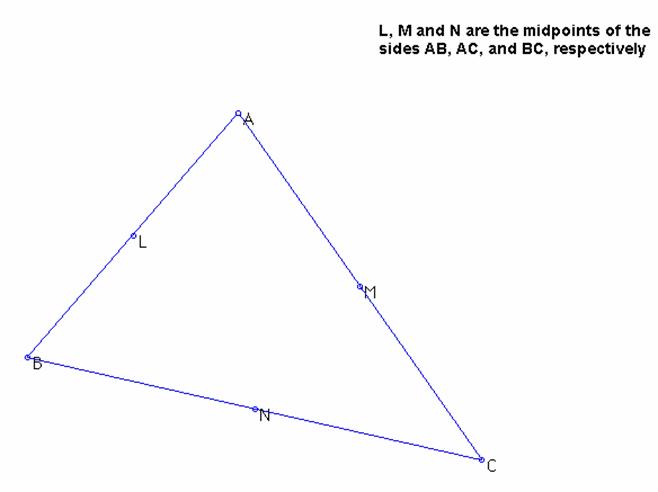
1) Begin by using Geometer's Sketchpad
to construct triangle ABC, as well as the midpoints of the sides.

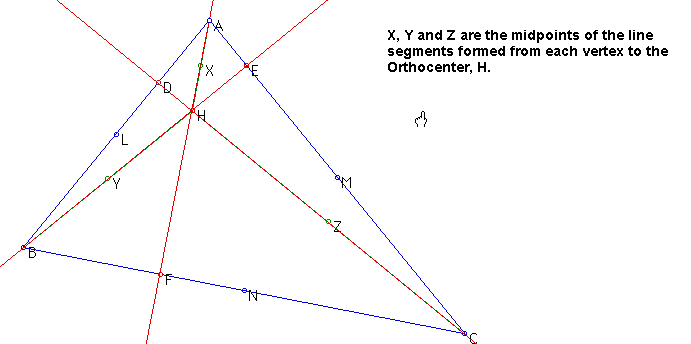
2) Now construct the feet of the altitudes of triangle ABC.
The point of intersection of these altitudes is known as the ORTHOCENTER.
3) Construct the third set of points.
These are the midpoints of the segments from each vertex to the Orthocenter.
4) At this point you should be able to
see the Circle. But how can we construct it? First we need to find the
Nine-Point Center.
In the figure below you can see that L, M, Y and Z form a rectangle with
an axis parallel to the base of triangle ABC. The intersection of the diagonals
of the rectangle, U, is the center of the Nine-Point Circle! We could just as easily construct a rectangle
with points X, Z, L and N, and the intersection of these diagonals would also
be U, the Nine-Point Center.
With U as the center, we can pick any point on the circle to construct
the circle.

5) Finally, we can see that the
CENTROID
(G) Intersection of the medians
(lines joining the vertices to the midpoints of the opposite sides)
CIRCUMCENTER
(O) Intersection of the perpendicular bisectors of
the sides; also the center of a circumscribed circle
ORTHOCENTER
(H) Intersection of the altitudes
(can be inside or outside)

RETURN to Janet’s Home page