Janet Kaplan __________________________________________________________________________________________________
The following is a library of scripts from Geometer's Sketchpad that can be used as templates for further work in GSP.
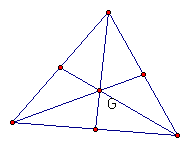
1) Centroid Intersection of the medians of a triangle. Medians are segments drawn from a vertex to the midpoint of the opposite side.
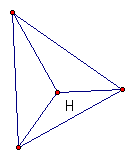
2) Orthocenter Intersection of the altitudes of a triangle. Can be inside or outside of triangle.
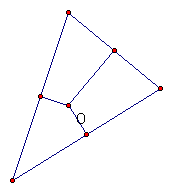
3) Circumcenter Intersection of three perpendicular
bisectors of the sides of a triangle. It is the center of a circumscribed circle.
4) Circumcircle This circle is constructed with the circumcenter as the center and the vertices of a triangle as points on the circle. It is also known as the circle around an inscribed triangle.
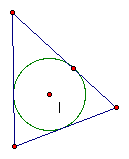
5) Incenter Intersection of three angle
bisectors of a triangle. It is the center of the inscribed circle and is
equidistant from all three sides of the triangle.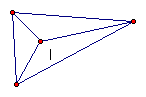 
6.) Incircle Also known as the inscribed circle, it is tangent to the sides of the triangle, with its center at the incenter.
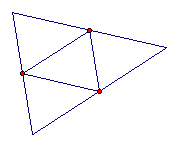
7) Medial triangle A triangle formed by connecting the midpoints of the sides of a
triangle. The length of the segments is one-half that of the original triangle.
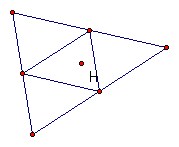
8) Orthocenter
of Mid-Segment Triangle Orthocenter of medial triangle
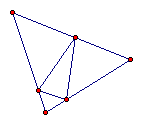
9) Orthic Triangle Triangle formed by connecting the segments of the feet of the altitudes.
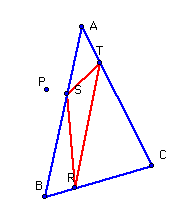
10) Pedal Triangle
The Pedal Triangle of any triangle is generated by taking a point P
anywhere on the plane, and constructing perpendicular lines from P to each side
of the triangle. The points of intersection of these lines with the sides of
the triangle become the vertices of the Pedal Triangle.
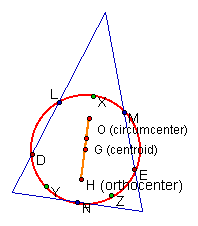
11) Nine Point Center
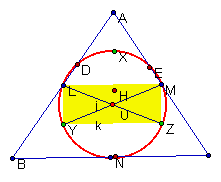There are several ways of
pinpointing the center from the
12) Nine Point Circle Circle that includes the three
midpoints of the sides of a triangle, the three feet of the altitudes, and the
three midpoints of the segments from the vertices to the orthocenter of the
triangle. (see diagram above)
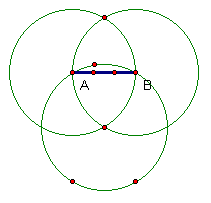
13) Trisecting a Line Segment It's not as straight forward as you might
think!
14) Equilateral triangle, given a side.
15) Square, given a side.
16) Isosceles Triangle, given base and
altitude.
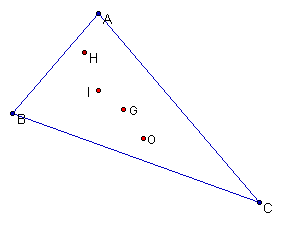
17) Triangle Centers The Centers of a triangle include the Orthocenter, the Circumcenter, the Centroid and the Incenter.
18) Euler Line This line contains the orthocenter, circumcenter and centroid of the triangle.
19) The Golden Ratio Isn't it beautiful?
________________________________________________________________________________________________________________________
RETURN to Janet’s Home page