
Janet Kaplan
The Star of David
_________________________________________________________________________________________________________
I have named this
construction the "Star of David" because that is, in fact, its shape
when the angles, lines and the resulting triangles are perfectly symmetrical.
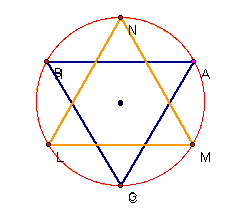
But our challenge is to
find the relationship between the angles of Triangle ABC and those of Triangle
LMN in all cases. We are given these parameters to begin our
construction:
Construct the internal
angle bisectors of acute Triangle ABC and extend them to meet the Circumcircle at points L,M and N,
respectively. Triangle ABC is colored blue; Triangle LMN is colored orange. For
a GSP construction that can be manipulated, CLICK HERE.
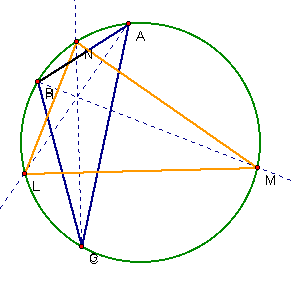
Go into the GSP
construction of the Star of David and you will notice that the angles of the
triangles have been measured. Move the vertices of the blue triangle (ABC) all
around to see the angle measurements change. Only these vertices can be moved,
as the vertices of the orange triangle are dependent upon the construction of
the blue. Make both triangles equilateral by getting as close as you can to 60
degree measurements for each angle. Its symmetry is beautiful, but it doesn't
tell us anything about the relationship between the angles of the two
triangles.
So what is the
relationship? I began with equilateral triangles and changed the size of the
angles from there. I noticed that as I increased the size of one of the blue
angles, the size of the corresponding orange angle decreased by a factor of
one-half. For example, when I increased <A by 20 degrees to 80 degrees, and
kept <B and <C constant, <L (its opposite, so to speak) decreased by
10 degrees to 50 degrees. Decreasing <A to 40 degrees increased <L by 1/2
or 10 degrees.
Interestingly, when I moved
any of the blue vertices such that the size of the orange angles changed, the
opposite thing happened! That is, increasing orange <M by 20 degrees, made
its ‘complement’ blue angle <B decrease by a factor of 2 (40 degrees) to 20
degrees.
The following chart
diagrams this relationship.
Change in Blue Angle Resulting
Change in
Increase Decrease by factor of 1/2
Decrease Increase by factor of 1/2
Change in
Increase Decrease by
factor of 2
Decrease Increase by
factor of 2
There are additional
observations that follow directly from the above. When the size of one angle is
changed, the other two angles in the same triangle adjust as well, such that
180 degrees are preserved. For that matter, as <B and <C decrease to
comply with the increase of <A, their complements in the orange triangle
<M and <N increase, taking up the degrees lost by <L. The relationship
is perfectly balanced in the sense that the 2:1 ratio between the blue angles
and their complimentary orange angles continues to hold regardless of how the
shapes of the triangles change.
We also know that as the
size of the inscribed angles change, the arc that they subtend changes
accordingly. That is, an angle increasing from 60 to 80 degrees will now
subtend an arc of 160 degrees, while its complimentary angle will subtend an
arc of 100 degrees.
_________________________________________________________________________________________________________
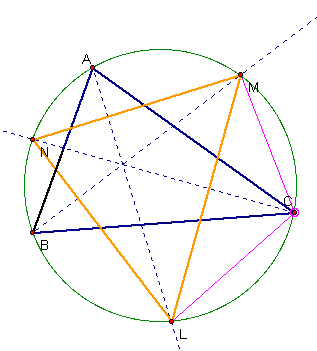
From our observations we
can see there is a 2 to 1 relationship between the angles in the two triangles.
How can we prove this to be the case?
PROOF
Construct segments LC and
MC. Remember that the dashed blue lines are the angle bisectors of the blue
triangle.
Arc LC is subtended by both 1/2 <A and a
portion of <N. Therefore, 1/2 <A and that
portion of <N are congruent.
Arc MC is subtended by both 1/2 <B
and the other portion of <N. Therefore, 1/2 <A
and that portion of <N are congruent.
From this it follows that <N
= <A + <B.
We also know that 90
degrees = 1/2 (<A + <B + <C) or 180 - <C = <A + <B or 90 -
1/2 <C = <A + <B = <N.
Now that we have the basic
equalities set, if we increase <N by 10 degrees, such that <N' = 70,
then 90 - 1/2 <C must also equal 70. This can only be true when <C is
decreased by 20 degrees, such that <C' = 50 degrees.
________________________________________________________________________________________________________