Janet Kaplan

PEDAL TRIANGLES

________________________________________________________________________________________________________________________

Let triangle ABC be any triangle. Construct a point P anywhere in the plane, and construct perpendicular lines from P to each side of ABC. Locate points R, S and T as the intersections of the sides of ABC and the perpendicular lines. Extend the lines of ABC in order to do so, if necessary.

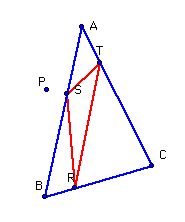Triangle RST is the Pedal Triangle for Pedal Point P. Note that P can be anywhere in the plane, either inside or outside of ABC.

CLICK HERE to see an initial Pedal Triangle construction which can be manipulated.

_________________________________________________________________________________________________________

As you move Pedal Point P all around, and adjust the size and shape of triangle ABC, you will notice that the Pedal Triangle occassionally degenerates into a straight line segment. That is, all three vertices of RST become collinear. When this occurs, it is known as the Simson Line. What are the conditions under which this happens?

It looks as if Point P has to be fairly close in towards the sides of ABC, and it definitely occurs when Point P lands on any of its vertices. Any conjectures?

In fact, In 1797 William Wallace proposed the following theorem. "The pedal triangle of a point P with respect to triangle ABC degenerates into a straight line if and only if P lies on the circumcircle of ABC." R, S and T are collinear only when P is on the circumcircle, and P is on the circumcircle only when R, S and T are collinear.

CLICK HERE for a GSP demonstration of this fact.

______________________________________________________________________________________________________________

We're going to look a little further into the patterns that are formed by pedal triangles.

Locate the midpoints of the sides of the Pedal triangle RST. Construct the circumcircle of triangle ABC, that is, a circle with the center at the circumcenter of triangle ABC and arc at the vertices. Now merge Point P onto this circumcircle. Trace the paths of the three midpoints as you animate Point P around the circumcircle. What are the paths?

CLICK HERE to see the animation.

The paths are ellipses in which the major axis is along the same vector as the angle bisector of each vertex of triangle ABC! And the length of each major axis is equal to each of the altitudes of ABC. Interesting! This would be a point of further study for me. I'd like to explore the mathematics behind this phenomenon.

______________________________________________________________________________________________________________

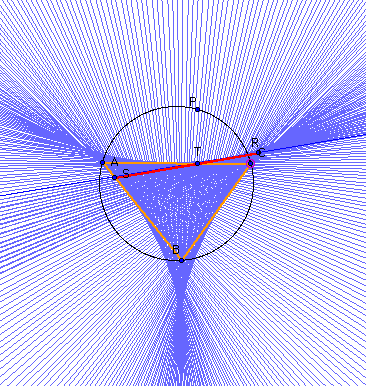
This next picture I call "the hammock". It is, in fact, the envelope of the Simson Line as the pedal point P is moved around the circumcircle. Construct lines over the line segments forming the sides of triangle RST, and mark them for tracing. Then animate point P again for its journey around the circumcircle. It makes a beautiful picture……CLICK HERE to see the animation in progress.

______________________________________________________________________________________________________________

RETURN to Janet's Home page