Janet Kaplan

Final Assignment

____________________________________________________________________________________________

Consider any triangle ABC. Select a point P inside the triangle and draw lines AP, CP and BP extended to their intersections with the opposite sides in points D, E and F, respectively.

This investigation will explore the line segments of the sides of ABC which have been generated by the lines going through P. We will make a conjecture about their relationship and prove it by using, among other things, the sub-triangles formed by the lines.

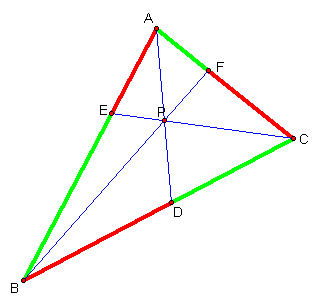
First we will explore line segments created by the extension of AP, CP and BP to D, E and F, respectively. By measuring the lengths of the segments, we notice that (AF)*(DC)*(BE) = (FC)*(DB)*(EA) for any location of P inside ABC, and regardless of whether ABC is acute or obtuse. By the same token, the ratio of (AF)*(DC)*(BE) to (FB)*(DB)*(EA) is always one.

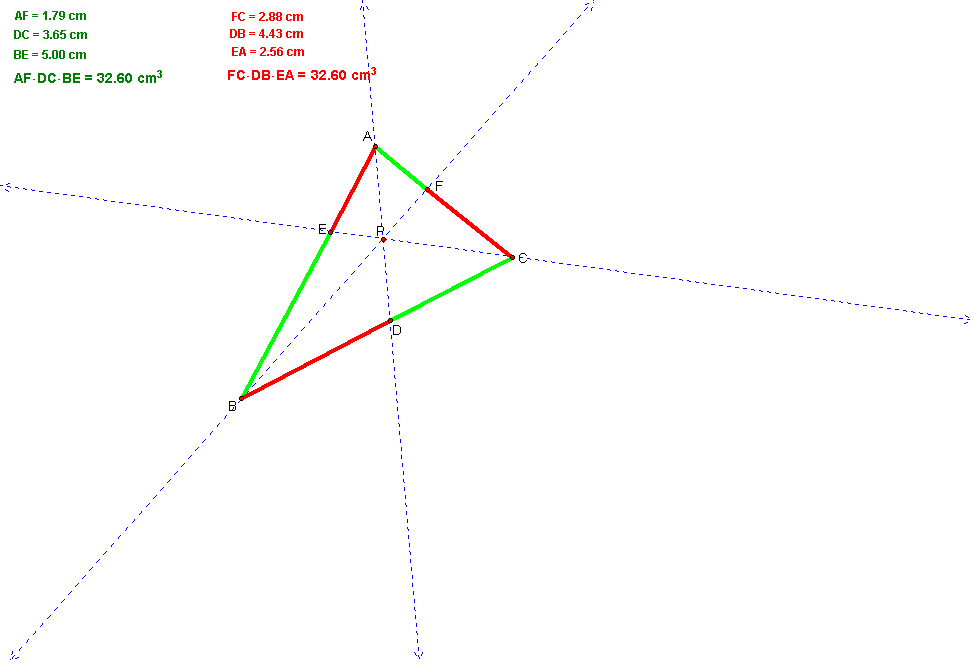
CLICK HERE for a GSP file in which you can move point P inside ABC yourself. Notice that the product of the red line segments always equals the product of the green line segments.

Actually, this is a theorem, known as Ceva’s Theorem. It defines the segments through P from each vertex to the opposite sides of the triangle as Cevians and states: Given any triangle ABC with a point P in the interior, the product of the ratios of the pairs of segments formed on each side of the triangle by the intersection point is equal to one, where the ratios are taken in the same orientation on each side. Further, if the ratio formed by any three Cevians is equal to one, then the three Cevians are concurrent.

Stated algebraically, (AF/FC)(BE/EA)(DC/DB) = 1 or (AF)(BE)(DC) / (FC)(EA)(DB) = 1

Notice that this is the case with our triangle ABC and the arbitrary interior point P.

Unlike many relationships in Geometry, this result is not intuitive to us. Let us prove this conjecture and Ceva’s Theorem.

We begin our proof by constructing a line parallel to BC, going through A. We then extend the lines CE and BF such that they intersect this parallel line at G and H, respectively.

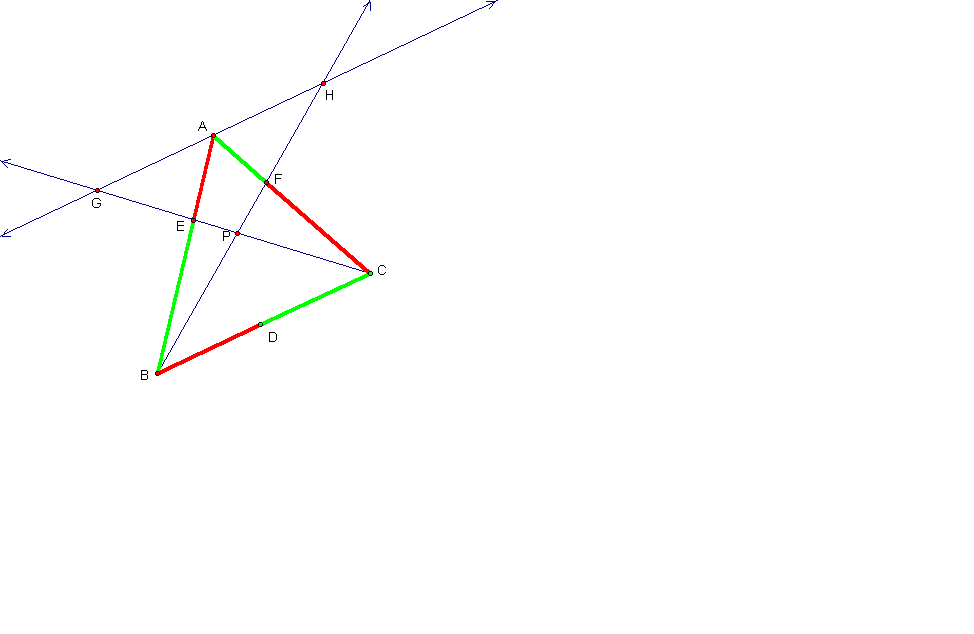
By constructing this parallel line, we have generated four pairs of similar triangles. Two pairs each are outlined in the first and second diagrams that follow.

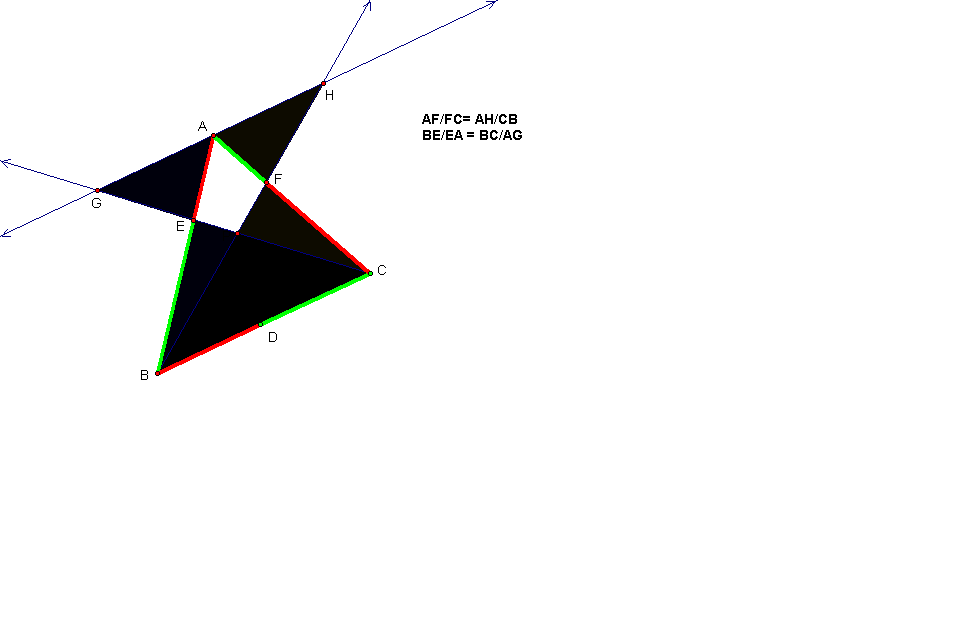
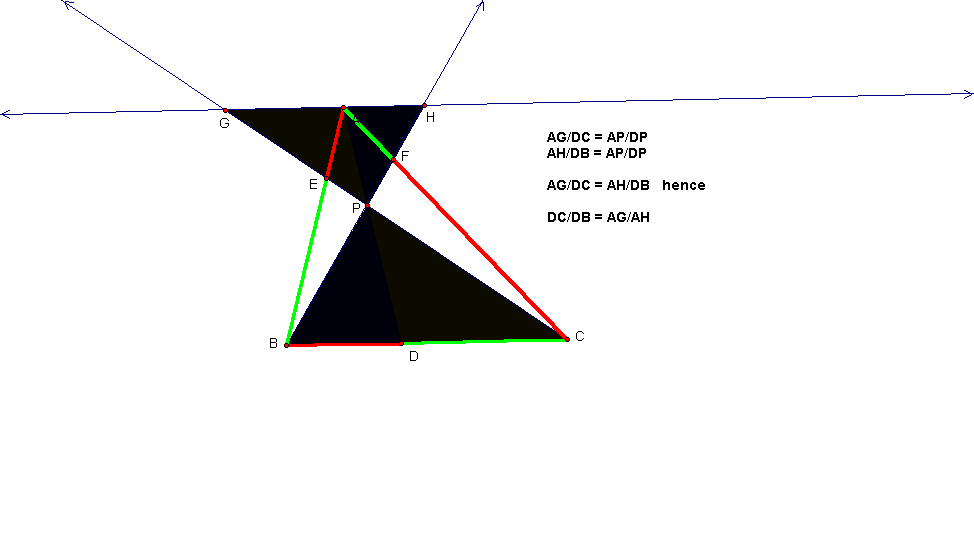
With similar triangles we know that corresponding sides are proportional to each other. The proportional relationship between each pair of similar triangles is indicated in the captions included with the diagrams above.

We are most interested in the identities that involve the segments of the sides of triangle ABC, and so throughout our analysis they have been emphasized and color-coded to match the diagrams.

Using algebra, we multiply the left sides of the identities stemming from the similar triangles, and set them equal to the product of the right sides of the same identities. That is,

(AF/FC)(BE/EA)(DC/DB) = (AH/CB)(BC/AG)(AG/AH)

By taking specific measurements listed below, we confirm that both sides of this equation are equal to each other, and that their value is equal to one.

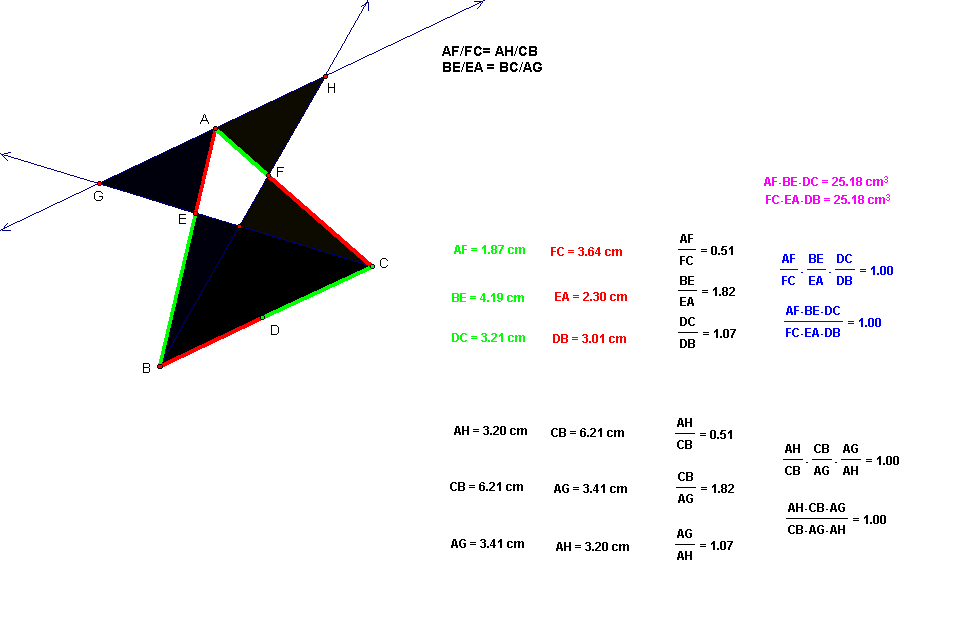
Since the value of (AF/FC)(BE/EA)(DC/DB) = 1, the values of (AF*BE*DC) and (FC*EA*DB) are equal to each other.

This proves our original conjecture: (AF)*(DC)*(BE) = (FC)*(DB)*(EA)

** I received help on this proof from www.cut-the-knot.org/Generalization/ceva.shtml

Can this result be generalized so that point P can be outside the triangle? See for yourself by CLICKING HERE.

When P is inside triangle ABC, the ratio of the areas of triangle ABC and triangle DEF is always greater than or equal to four. Notice that it is exactly equal to four when D, E and F are the midpoints of their respective sides, and therefore P is the centroid of triangle ABC. CLICK HERE for a GSP demonstration of this.

RETURN to Janet’s Home page