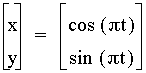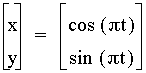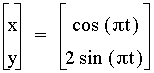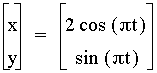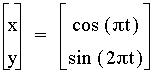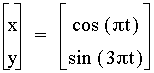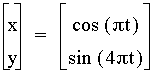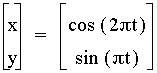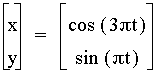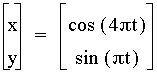Assignment
10
Parametric
Curves
A parametric
curve in the plane is a pair of functions:
x=f(t)
y=g(t)
where
the two continuous functions define ordered pairs (x,y). The two
equations are usually called the parametric equations of a curve.
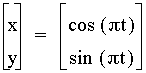
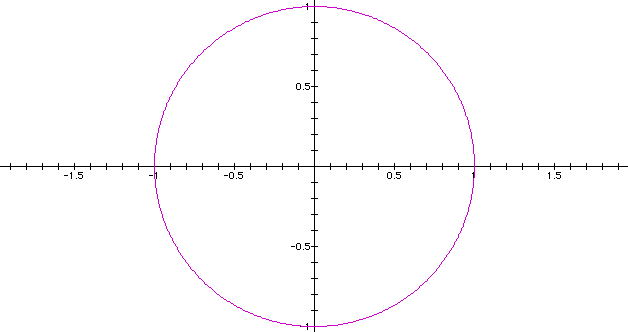 This
first graph is one of the simpler graphs. The center is (0,0)
and the radius is 1.
This
first graph is one of the simpler graphs. The center is (0,0)
and the radius is 1.
There
are many different alterations that we can make to the graph.
I will begin by changing coefficient in front of the sine function.
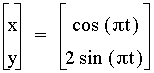
 Notice
that this change elongates the graph and it now has the characteristics
of an ellipse with center still at (0,0) and a major vertical
axis with vertices at (0,2) and (0,-2) and co-vertices at (1,0)
and (-1,0).
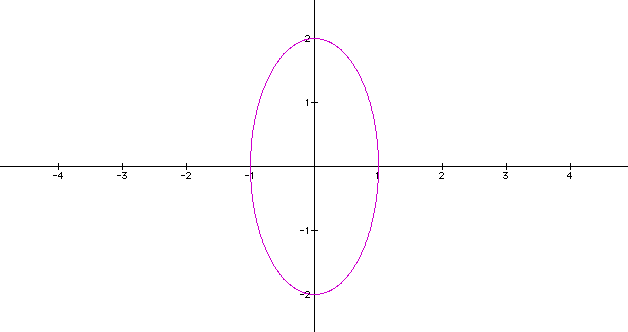
Notice
that this change elongates the graph and it now has the characteristics
of an ellipse with center still at (0,0) and a major vertical
axis with vertices at (0,2) and (0,-2) and co-vertices at (1,0)
and (-1,0).
We
would expect a change in the coefficient for the cosine to have
a similar effect, but on the horizontal axis.
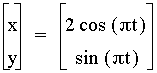
 So,
the center of this ellipse is (0,0). It has a major horizontal
axis with vertices at (2,0) and (-2,0) and co-vertices at (0,1)
and (0,-1).
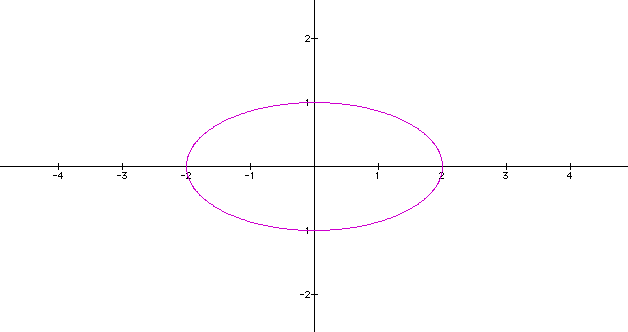
So,
the center of this ellipse is (0,0). It has a major horizontal
axis with vertices at (2,0) and (-2,0) and co-vertices at (0,1)
and (0,-1).
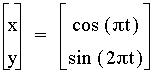
 When
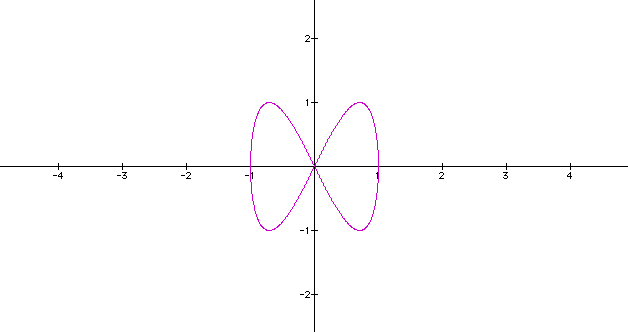
the sine is changed from
When
the sine is changed from  to
to  ,
we see the graph is changed to a bowtie curve.
,
we see the graph is changed to a bowtie curve.
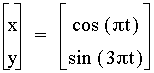
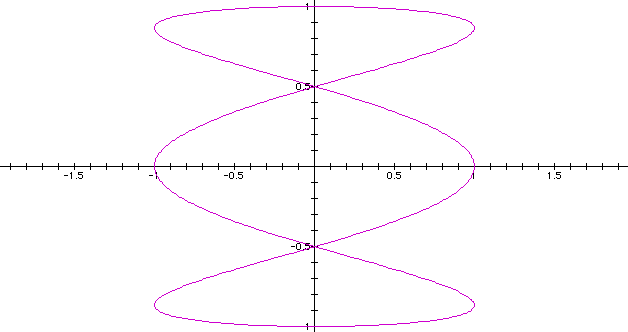
 When
we increase the coefficient to a 3, there are now three loops.
When
we increase the coefficient to a 3, there are now three loops.
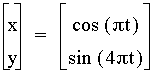
 Again,
multiplying
Again,
multiplying  by a larger number for the sine,
increases the amount of loops to the number we multiplied by.
by a larger number for the sine,
increases the amount of loops to the number we multiplied by.
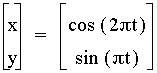
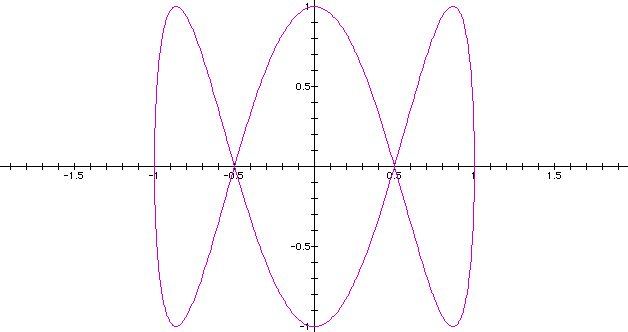
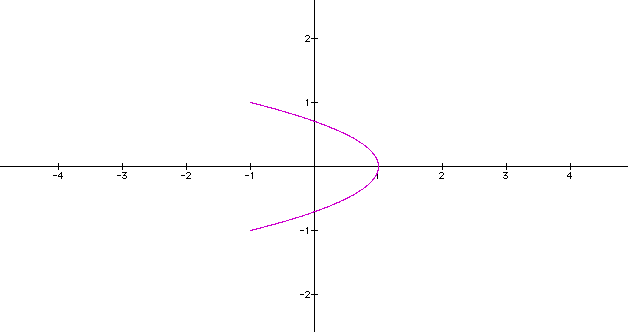 When
the same alteration is made for cosine, we get a parabola.
When
the same alteration is made for cosine, we get a parabola.
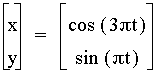
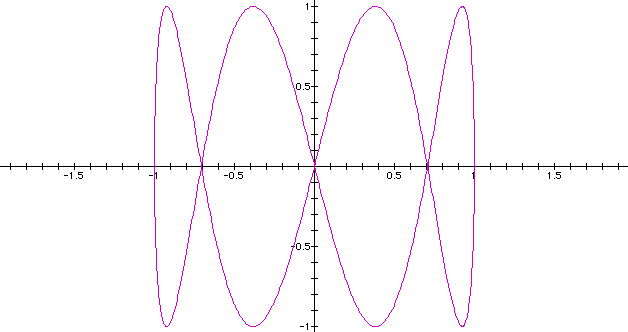
 However,
multiplying
However,
multiplying  by a 3 for cosine, we get a similar
pattern with 3 loops.
by a 3 for cosine, we get a similar
pattern with 3 loops.
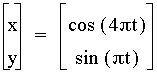
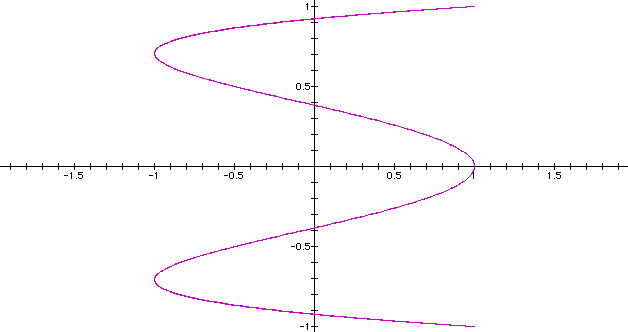 Multiplying
Multiplying
 by a 4 we see a similar pattern
to what happened when the coefficient was a 2.
by a 4 we see a similar pattern
to what happened when the coefficient was a 2.
Conclusion
from this investigation: When the coefficient is changed in front
of the sine function, it will create the same amount of loops
as what the coefficient is. When the coefficient is changed for
the cosine function, we will get a continuous graph for odd coefficients
and a discontinuous graph for even coefficients.
Another
exploration that is interesting is when rational numbers between
0 and 1 are the multipliers.
Click
HERE to see what happens
when we make this change in the sine function.
Chlick
HERE to see what happens
when we make this change in the cosine function.
return