Assignment 7

TANGENT LINES

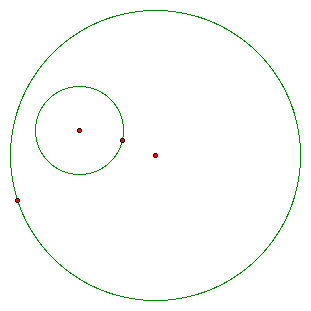Gives these two circles, I will create a circle that is tangent to both of them.

I will first construct a radius in the smaller circle.

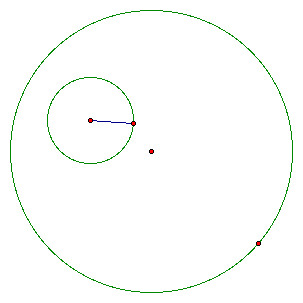
Next I will construct a line through the center of the larger circle.

Now I will copy the smaller circle so that the center the point on the top of the larger circle .

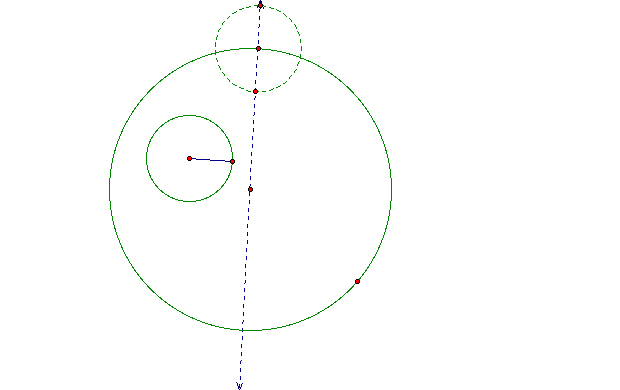
Now I will connect the top point of the new circle with the center of the smaller circle.

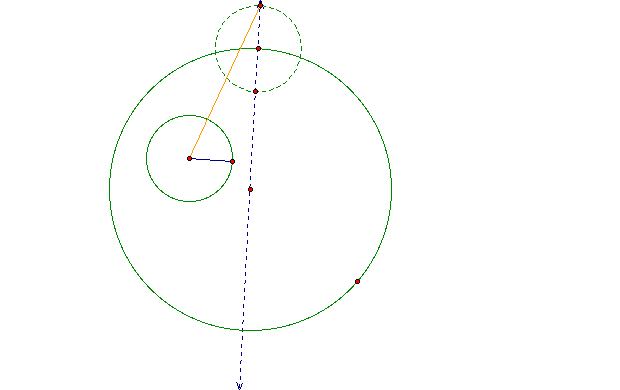The result is the orange segment.

I will now create the perpendicular bisector of the orange segment. The intersection of the perpendicular bisector and the dashed blue line will be the center of the tangent circle.

The result is this dotted red circle.

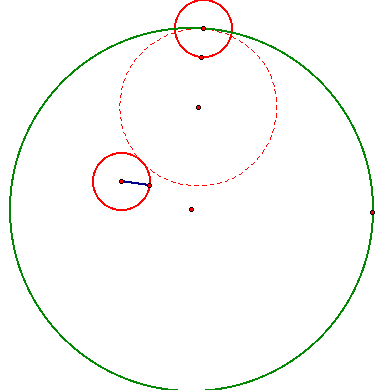
Through the construction of several perpendiculars, I have created the inside dotted circle, which is tangent to both initial circles.

Click here to see what happens when the circles are rotated around each other and the point of intersection is traced.

Here is the still picture of what you just saw.

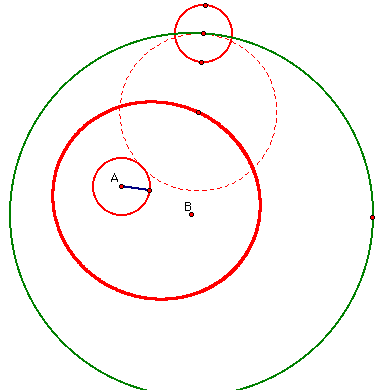So, as you can see, the traced center of the tangent circle creates an ellipse. This seems to make sense since points A and B would be considered foci. This follows the definition of an ellipse.

What happens if the two circles initially intersect eachother?

After constructing the same process as above, check out the animation for this example by clicking HERE.

Here is the still picture of the locus of points.

The red ellipse is the traaced object. Again we can see that the foci must be the two points near the ellipse in the interior.

The last situation is where the circle is outside the initial circle.

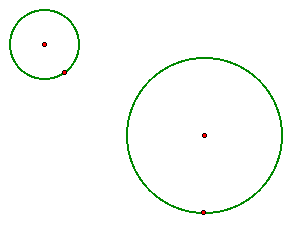
I will construct the circle tangent to both circles in the same fashion that I did above.

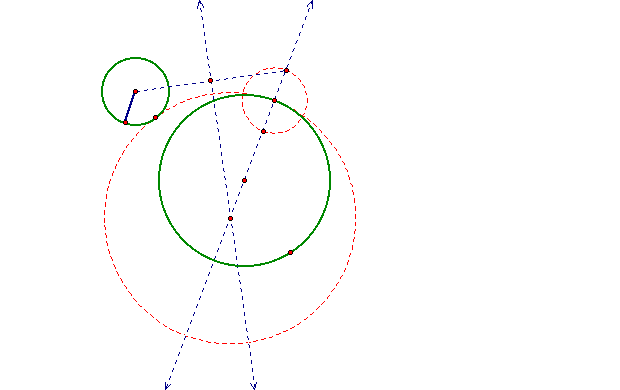Notice that the red dotted circle is tangent to both green circles.

Click HERE to see the locus when the intersection is traced around the circle.

Here is the still picture of what you just saw.

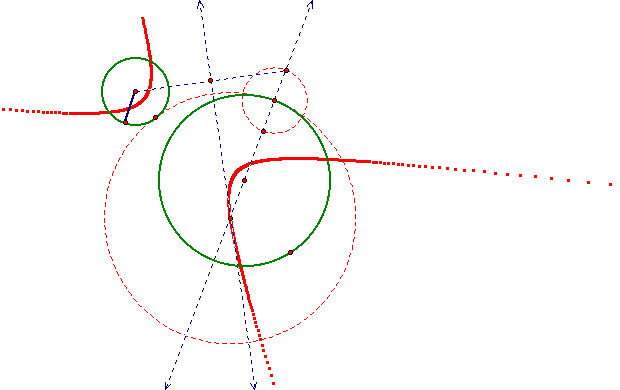In this situation we get a hyperbola instead of an ellipse. So here we can see that the foci must be the centers of the two green circles.

return