Assignment 8

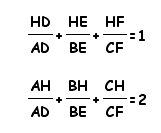
Given triangle ABC with Orthocenter H and points D, E, anf F are the feet of the perpendiculars from A, B, and C respectively.

Prove:

 

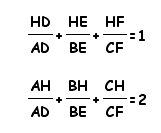
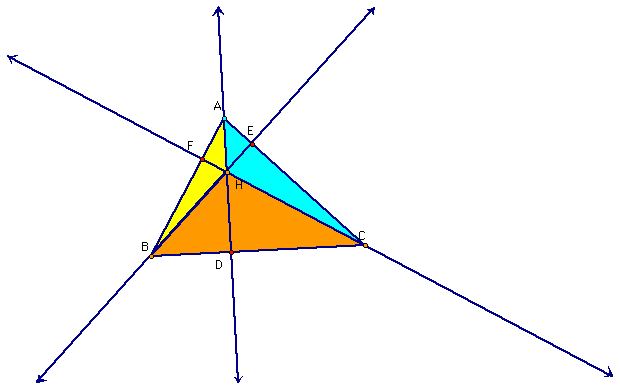
I am going to begin by comparing the areas of each shaded triangle to the whole triangle.

Here is the ratio of triangle BHC to triangle ABC:

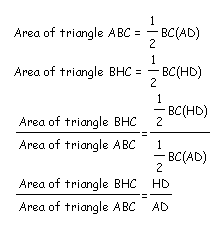
Here is the ratio of triangle AHC to triangle ABC.

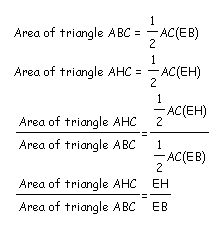
Here is the ratio of triangle AHB to triangle ABC.

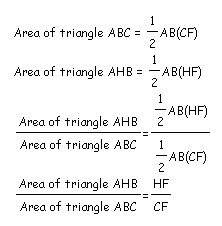
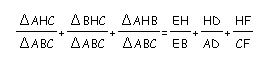
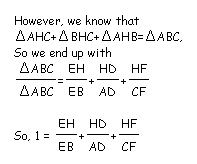
By using basic arithmetic, we can see that:

Let's now investigate (AH/AD)+(BH/BE)+(CH/CF)=2.

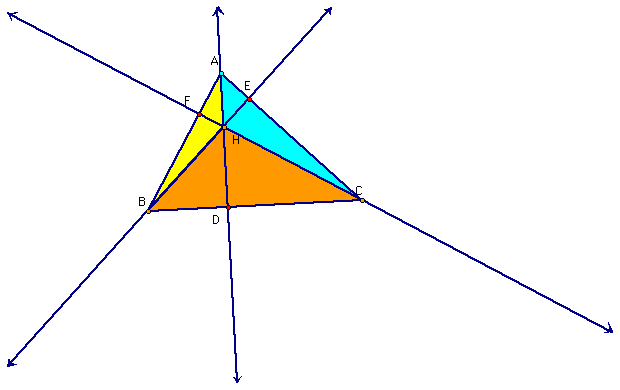
To prove this we need to take a look at the sum of some of these areas.


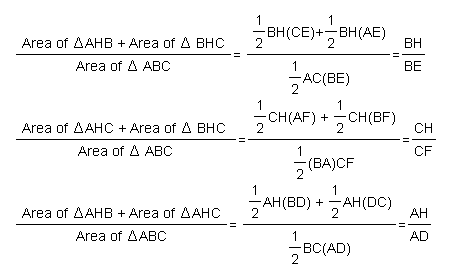
When we add these equations together we can see that the sum of the ratios will equal 2.

Now let's see what happens when ABC is an obtuse triangle.

 

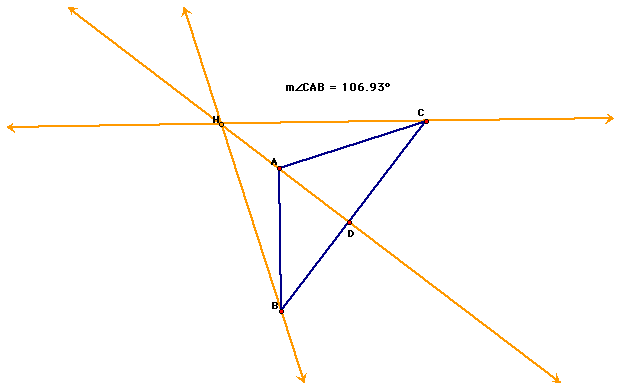
Notice that the Orthocenter falls outside of the original triangle. Does this mean that the relationship will remain the same? We can see that it would not remain the same from looking at the diagram. In fact, our points of intersection at E and F don't even occur.

 

 

return