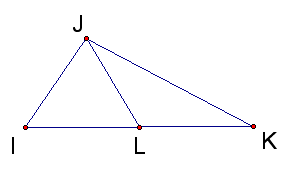
To bisect the area of a triangle, I will begin by constructing one median of the triangle.

JL is a median. Hence it cuts side IK in half. Therefore, IL = LK. Since the bases are equal for the two triangles and they have the same perpendicular height up to J, then their areas are equal.
Now I will attempt to trisect the area by constructing the other medians and their point of concurrency (The centroid).
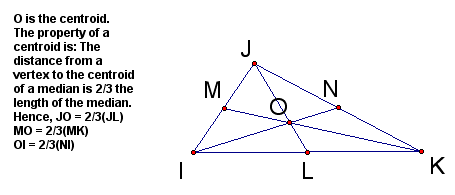
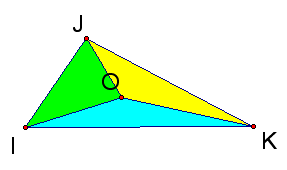
By creating the three medians, I have cut the area into 6 equal parts. But notice that (from what was mentioned above) That triangle IOL has the same area as triangle KOL, triangle JOM has the same area as triangle MOI, and triangle KON has the same area as triangle NOJ. By combining these three groups together, they each are 1/3 of the area of the original triangle, hence the figure below is the finished diagram of a triangle whosw area has been trisected.
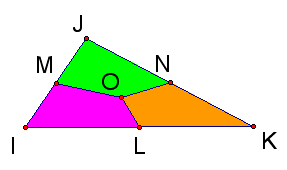
Connecting to the midpoints instead of the vertices would also trisect the area because you are just combining different groups of triangles together.
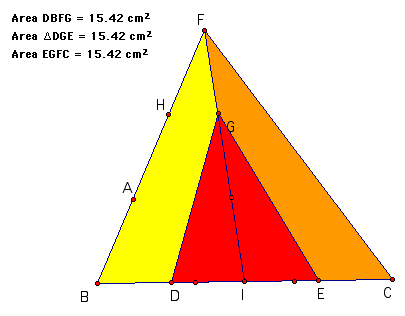
Here is another example of how to trisect the area of a triangle. In this example, the area is trisected into a triangle and two quadrilaterals. To do this construction, begin with any triangle. Construct the median to one side : FI. Then trisect the median using parallels to one of the sides. (notice, I trisected sides FB using circles with the same radius, then I just constructed parallel lines to BC through A and H to trisect the median.) Next I constructed the midpoints of BI and IC and called them D and E respectively. The resulting sketch shows that equal area result.
Another trisection that can be done follows below:

As you can see, the area of triangle HLM is 1/3 of the area of triangle HIG. This construction was done by constructing HM to HG is the ratio 1 to the square root of 3. I used a 30-60 -90 right triangle to construct the square root of three and then copied it on the larger triangle. My goal is to trisect the triangle, so I have one more construction to do.
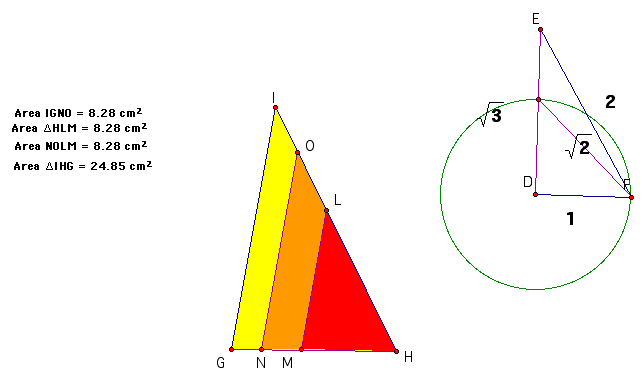
Here you can see that the area of the original triangle has been trisected into three equal areas. To do this construction, I constructed a 45-45-90 right triangle and copied the square root of two onto Side HG. Hence HN has the length of the square root of two. I used the right triangle in the upper right hand corner for my constructions of the suare root of three and the square root of two.