Remember, a probability is a number between __ and __.
Review: If you roll a fair die, what is the probability that you:
a.) roll a 2______
b.) roll an even number____
c.) roll a prime number____
d.) roll a 7_____
e.) roll a 1,2,4 or 6____
f.) roll a 1,2 and 3____
Geometric probability is the same idea.
Example 1:
Look at the segment below. AB is a segment that contains CD. If a point on segment AB is chosen at random, then the probability that the point is on CD = length of CD/length of AB.
![]()
Let AB = 12 and CD = 4. Then find the probability that the point you choose is on CD. Find the probability that the point you choose is not on CD.
Example 2:
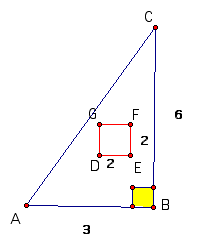
ABC is a right triange and DEFG is a square inside the triangle. Pretend you are thowing darts at the triangle. What is the probability that your dart would land on the square? What is the probability that it would not land on the square?
We would do this example using area. The probability that the dart lands on the square would be area of square/area of triangle.
The area of the square is ______.
The area of the triangle is_______.
The probability that the dart lands on the square is _______. While the probability that it doesn't is _______.
Examples of geometric probabilities can be found all over the place in the real world. For example, in darts, what is the probability that you hit the bullseye? Is it really likely? Or will it now happen very often?
Assignment: Find the measurements of a dartboard and determine the likelihood of hitting the bullseye. Be prepared to discuss your findings with the class.
**A bit of history:
Probability developed relatively late in the field of mathematics. It developed mostly for the insurance business. Insurance companies wanted to know if they should insure people based on the likelihood that they would die.
Comte de Buffon (1707-1788) was one of the first mathematicians to work with geometric probability. He came up with "the needle problem". Basically, the needle problem says to draw a pair of parallel lines where their distance is greater than or equal to the size of a needle. Drop the needle and record the number of hits (meaning the needle lands on the line). The ratio of 2 X number of hits to total drops will be an estimate of pi.
1. Try this experiment. Drop a needle 50 times. Record the number of drops and the number of hits.
2. We will pool our data together as a class to see if we get an estimate close to pi.
3. Click here to see a simulation of Buffon's needle problem.
4. Why do you think this
works? Explain your answer.
Go to assessment for this chapter