Part A.

To see the write up for EMAT 6680 click here.

Part B

Consider an abritrary triangle with a point p inside the triangle.

Construct the lines AP, BP, and CP and label the intersections with the opposite side D, E , F respectively.

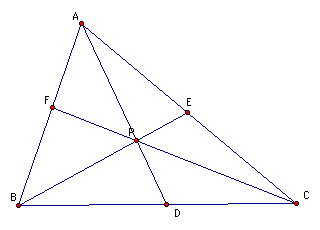
I conjecture that (AF)(BD)(EC) = (FB)(DC)(EA).

Proof:

Construct lines parallell to AD through B and C.

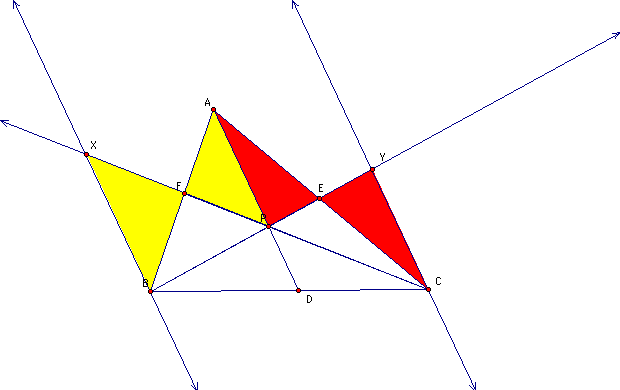
Angles PAF and XBF are alternate interior angles which means they are congruent. Angles AFP and XFB are vertical angles so they are congruents. By the Angle-Angle similarity triangles. AFP and BFX also CEY and AEP are similar.

Hence AF/BF = AP/BX and CE/AE = CY/ AP.

By a similar argument triangles BDP and BCY also BCX and DCP are also similar.

And BD/BC = DP/CY and BC/DC = BX/DP.

Multiplying

(AF/BF)(BD/BC)(BC/DC)(CE/AE) = (AD/BX)(CY/AD)(DP/CY)(BX/DP)

Simplifing yields

(AF)(BC)(CE)/(BF)(DC)(AE) =1

Therefore

(AF)(BC)(CE) = (BF)(DC)(AE).

Part C

I couldn't prove this.