
Exploring
graphs of y = a sin(bx + c)
Consider what hopefully is the familiar graph of the equation y = sinx below.
We see that this is a periodic function with
period 2 pi, amplitude of 1, and passes through the origin.
We note that this equation is a special case
of the general form: y = a sin(bx+c). In the graph above a = 1, b = 1, and c =
0. A natural question arises. How do different values for a, b, and c affect
the graph?
First, we'll look at varying a by fixing b and c at 1 and 0 respectively.
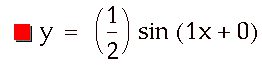
![]()
![]()
So we see that varying a changes the
amplitude of the sine curve but does not change the period or position of the
curve. In fact, we see that the value of a is the amplitude of the curve. So
what about negative values of a? A negative value for a produces a graph that is
a reflection of the graph for the corresponding positive value for a over the
x-axis. This is illustrated below.
![]()
![]()
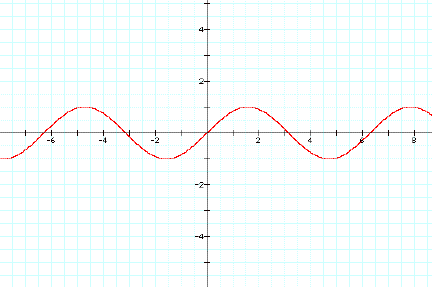
Next we will examine different values for b
by fixing a and c at 1 and 0 respectively.
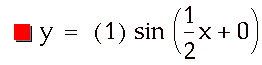
![]()
![]()
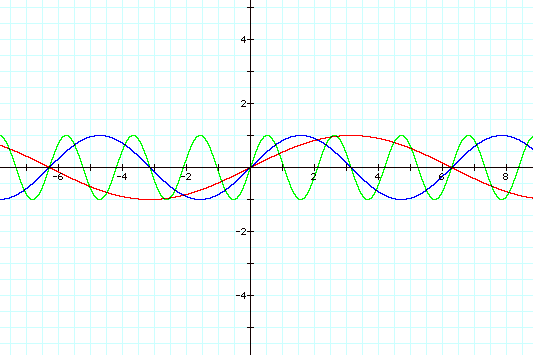
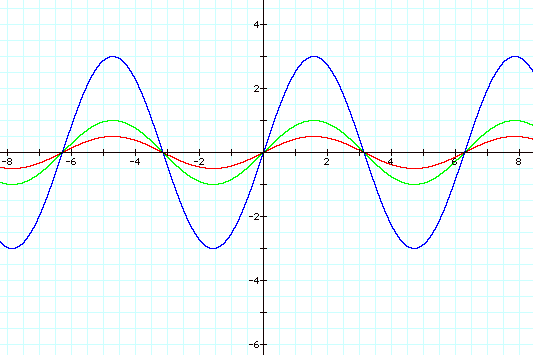
So now we see that changing b changes the
period of the sine curve alone. In fact, we see that the period is inversely
related to the value of b. When b = 1/2, the period of the curve is twice the
period when b = 1. Further, when b = 3, the period is 1/3 the period when b =
1.
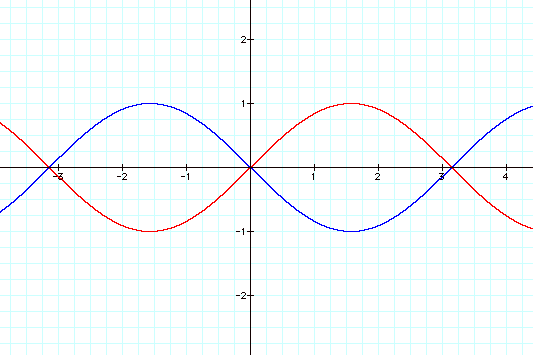
We again find that a negative value for b simply produces a graph that is the mirror image across the x-axis from the corresponding positive value for b. We illustrate this below.
![]()
![]()
Finally, we will look at varying the value for
c and see what effect it has on our graphs. We will again fix a and b at 1 and
1 respectively.
![]()
![]()
![]()
![]()
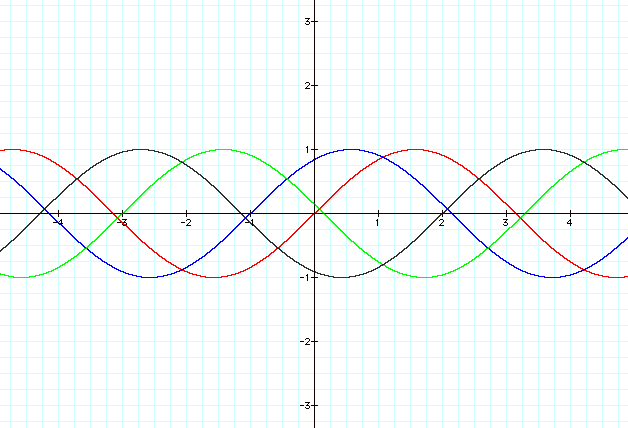
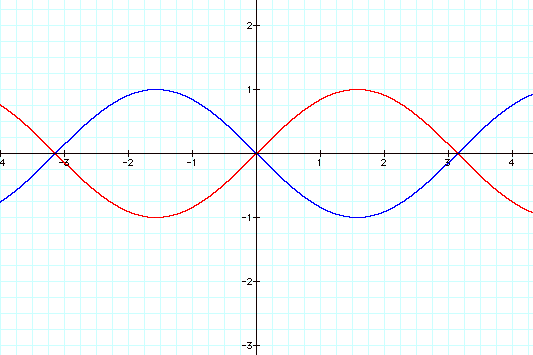
Now we see that changing c affects the
horizontal position of the sine curve. We can see that positive values of c
move the sine curve c units to the left while negative values of c move the
curve c units to the right.
So lets put what we have learned to the test.
Given the following equation,
y =
3/2(sin(2x-2))
what can we say about the amplitude, the
period, and the position of the graph relative to the graph of the equation y =
sinx?