Exploring the graph of x²+nxy+y²=9

Consider the graph of the equation x²+y²=9.

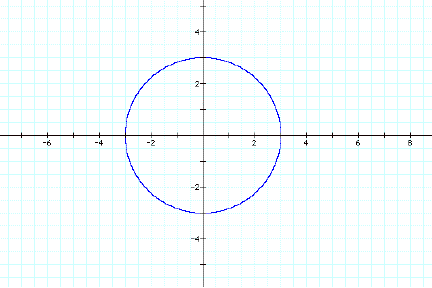
This is the graph of a circle centered at the origin with radius equal to 3. The equation x²+y²=9 can be thought of as a special case of the more general equation x²+nxy+y²=9 where n=0. Consider now some graphs of the general equation for different values of n.

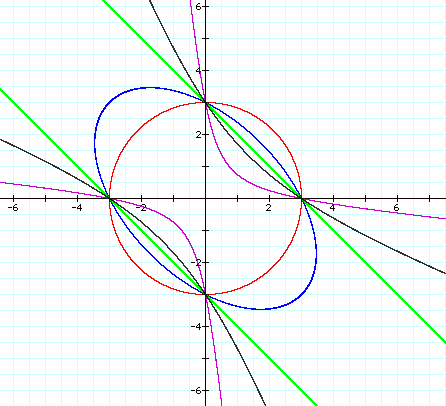
We get a series of ellipses (pointing in the direction of the II and IV quadrants) and hyperbolas (opening up towards the I and III quadrants). We note that all curves pass through the same 4 points: (3,0), (0,3), (-3,0), and (0,-3). The graph when n=2 suggests that this may be a critical value where the graph transitions from one kind of curve to another kind.

Note that, so far, we have only looked at positive values for n. Before we go further, let's look at the case where n takes on negative values.

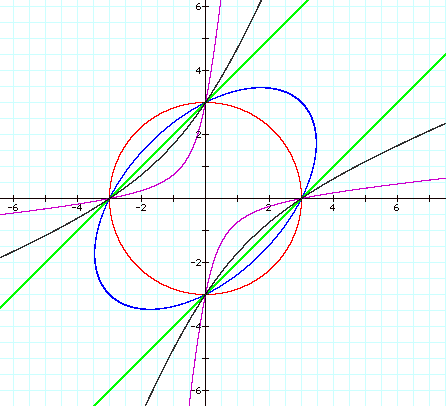
We see that we get the same curves simply reflected across the x-axis (or the y-axis). Now the ellipses point in the direction of the I and III quadrants and the hyperbolas open up in the direction of the II and IV quadrants. So we can limit our exploration to positive values of n and know that we can extrapolate our results by reflecting over either axis.

Now lets get back to looking at what happens when n=2. First, let's examine the curves when n varies from 0 to 2.

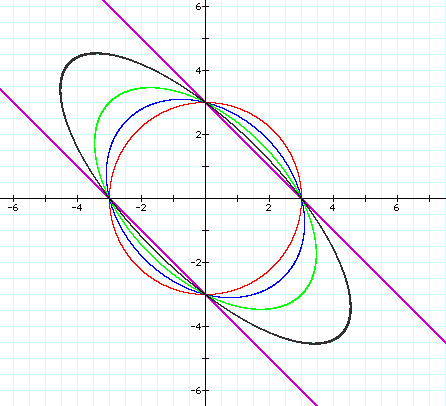
So starting with our original circle when n=0, we see that the curves become an increasingly stretched ellipse until n reaches 2. The graph when n=2 looks like two parallel lines with the scale set as it is. In fact, it is still an ellipse that has just been stretched out to infinity.

We will now look at the curves when n is greater than or equal to 2.

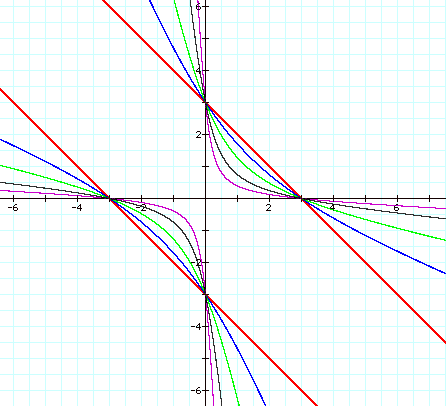
So we see that as n increases, for n>2, that we get hyperbolas with a sharper vertex that gets closer and closer to the origin.