
The
9 Point Circle and its Center
The Nine-Point Circle for any triangle is the
circle passing through the three midpoints of the sides of the triangle, the
three feet of the altitudes of the triangle, and the three midpoints of the
segments from the respective vertices to the orthocenter.
To construct this circle, we first construct D ABC. We then construct the medial triangle of D ABC. The vertices of this triangle are by definition the three
midpoints of the sides of D ABC. We can label these points
D, E, and F. Next, we construct the orthic triangle of D ABC. The vertices of this triangle are the feet of the altitudes of D ABC. We can label these points G, H, and I. Finally, we construct the
orthocenter of D ABC, and then the mid-segment triangle with respect
to this orthocenter. We can label these vertices J, K, and L. Note that the
orthocenter of a triangle is normally labeled H, but it is convenient for this
write-up to label it M.
So we have the following construction:
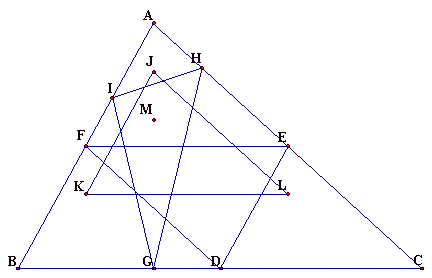
The nine vertices of these three inscribed
triangles lie on the nine-point circle. We only need to locate the center of
this circle to enable us to construct it.
If we construct the circumcircle of each of
the inscribed triangles, we note that all three circumcircles overlay each
other. We label the common circumcenter N. Since all nine points that we are
interested in lie on any one of the circumcircles, we conclude that the center
of the nine-point circle is in the same location as the circumcenter for any of
the inscribed triangles.
So we now have the following construction:
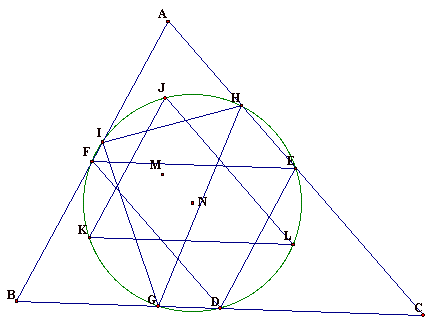
We can now hide the three inscribed triangles
and their circumcircles. We can then construct the nine-point circle using
point N as the center and any of the vertices of the now hidden triangles as a
point on the circle.
We finally have our nine-point circle:
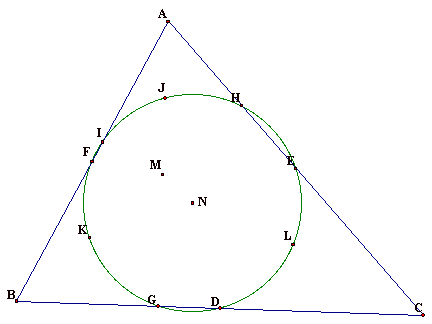
Since we have already constructed the
orthocenter (point M), if we continue and construct the centroid and
circumcenter of D ABC, we can explore the relationship between these
points and the center of the nine point circle for different shaped triangles.
We will label the centroid O and the circumcenter P.
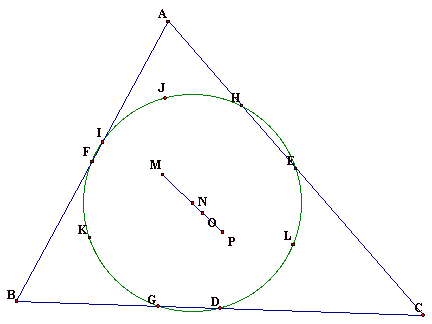
We note that a single line can be drawn
through all 4 points (M, N, O, and P). Using GSP, we can see that for different
acute triangles the nine point circle center is always inbetween the
orthocenter and the centroid and is always on the opposite side of the centroid
from the circumcenter.
Click here for a GSP file to try yourself.