Should we take a penalty?

From time to time, while watching college football you hear the commentators suggest that a team would be wise to take a penalty before attempting to kick a field goal if they must kick from the hash marks. The argument is that if the kicker is too close to the uprights, then he will have a poor angle to kick from. But does this suggestion hold up to mathematical scrutiny? We'll use Geometers Sketchpad (GSP) to attempt to shed some light on this subject.

So the first step was to find the necessary dimensions of the college football playing field. From the official website of the NCAA the following dimensions were found. The uprights are 18.5 ft wide and are equidistant from both sidelines. The playing field from sideline to sideline is 160 ft. The hash marks are 60 ft from the nearest sideline. So the center of the uprights is 20 ft from either hash mark.

So with this information, we're ready to construct a figure in GSP and begin our investigation. I decided to scale the dimensions by converting to inches and then dividing by 100. I first constructed a segment AB that was 2.22 scaled inches in length to represent the uprights (18.5 ft multiplied by 12 inches divided by 100). I constructed the midpoint of AB and labeled it E. From E, I constructed segment EC that was approximately 2.40 scaled inches to represent the distance from the center of the uprights to a hash mark (20 ft multiplied by 12 inches divided by 100). I then constructed a line perpendicular to AB through the point C. I then picked an arbitrary point D (representing the spot for the field goal attempt) on the perpendicular line and constructed segments AD and BD.

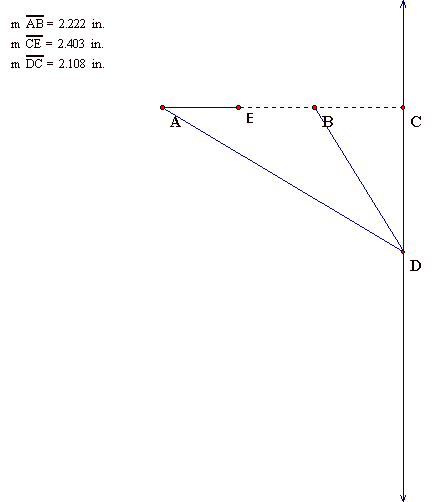
So the length of segment DC is the distance of the attempted field goal. The angle ADB is the angle we are interested in. What is the length of DC when this angle is at a maximum?

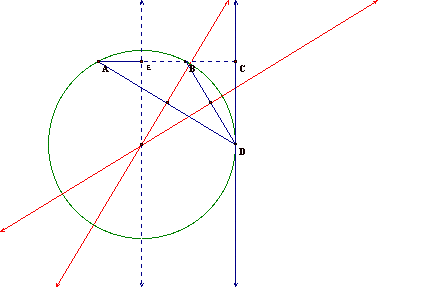
Let's try and answer this question by constructing a circle through A, B, and D. We can do this by first constructing the midpoints of AD and BD. Then we construct perpendicular lines to AD and BD respectively through their midpoints. The intersection of the two perpendicular lines locates the center of a circle through A, B, and D. This construction is shown below.

So how did this help us? Well the angle we are interested in maximizing (angle ADB) is 1/2 the measure of the arc AB. This is true because angle ADB is an inscribed angle and arc AB is its intercepted arc. So if we maximize arc AB, we will also maximize angle ADB.

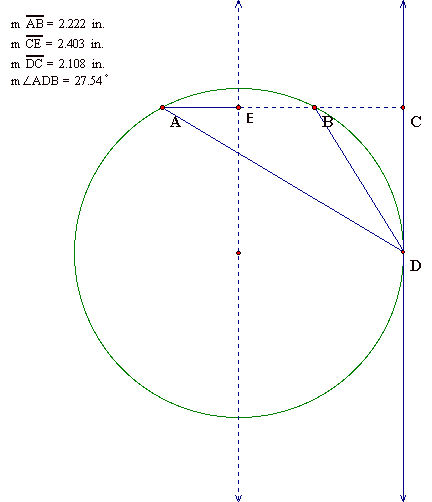
Remember that we have fixed points A and B, and only allow point D to move along line CD. So we can see that arc AB (and therefore angle ADB) is at a maximum when our constructed circle is smallest; which occurs when the circle is tangent to line CD. GSP can measure the angle ADB to double-check our conclusions.

Click here for a GSP file to try yourself.

Now back to the question that started this investigation. Notice that the measured distance of segment CD is 2.108 scaled in. If we convert this length back to feet, we see that this distance on the football field is approximately 17.5 ft or less than 6 yards! But the uprights are located 10 yards into the endzone. This means that the maximum angle to kick a field goal from the hash marks occurs when attempting to kick from about the negative 4 yard line!

Intuitively it seems that backing away may give a kicker a better angle to kick from. But in reality every yard he backs away from the endzone, he decreases his angle to the uprights. In addition, the kicker must now also kick a longer distance, probably at a lower trajectory with a higher risk of being blocked. Any advantage in taking a penalty before kicking would be purely psychological.