Altitude Ratios

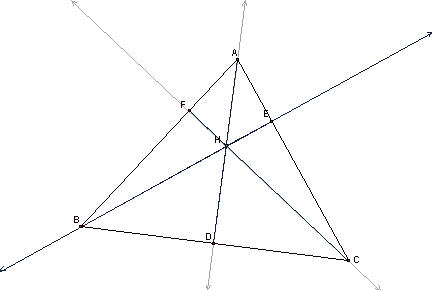
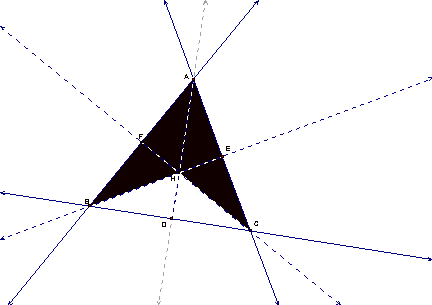
Suppose I construct an acute triangle ABC. I then locate the orthocenter H by constructing the altitudes from each vertex. The orthocenter is the intersection of these altitudes. I then label the feet of the altitudes D, E, and F. Below is a picture of this construction.

I am interested in the sum of the following ratios:

(HD)/(AD) + (HE)/(BE) + (HF)/(CF)

Using the measure tool in GSP I can calculate the sum of the ratios of these segments. I find that for any shape of the acute triangle the sum of the ratios always equals one.

Click here for a GSP file to try yourself. Why is this so?

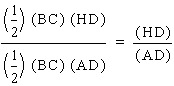
Well, let's consider one of the ratios initially. The segment AD is of course an altitude of triangle ABC while the segment HD is the altitude of triangle HBC. Since these two triangles share the same base, the ratio of the areas of HBC to ABC is equal to the ratio of the segments HD to AD.

It follows then that we can apply this same logic to the ratios (HE)/(BE) and (HF)/(CF) to write:

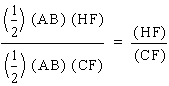
and

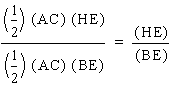
So we have the following picture where the yellow triangle is HBC, the blue triangle is HAC, and the red triangle is HAB:

So

=

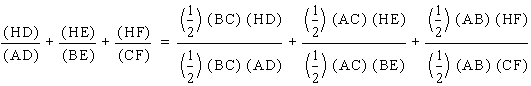= 1.

Now consider the sum of the ratios:

(AH)/(AD) + (BH)/(BE) + (CH)/(CF)

Again using the measure tool in GSP I can calculate the sum of the ratios of these segments. I find that for any shape of the acute triangle the sum of the ratios always equals two.

Click here for a GSP file to try yourself. Let's try and prove why this is so.

Again we'll examine a single ratio and then apply it to the other two ratios So based on the logic above, I want to try and relate the ratio (AH)/(AD) to the ratio of some areas of triangles. . I know that AH is AD-HE. So I can think of AH as being analogous to the area of ABC minus the area of HBC. Visually it looks like this:

So applying this logic:

(AH)/(AD) + (BH)/(BE) + (CH)/(CF) is equal to

which is equal to

which is equal to

which is equal to

which is equal to 3-1 = 2.

The reader perhaps has observed that none of the above holds when triangle ABC is obtuse. When this is the case the orthocenter H is located outside of ABC. We in fact see that the more obtuse ABC is, the further outside the triangle the orthocenter is located, the greater the sums of the ratios of segments discussed above.