Triangle Ratios

Consider a triangle ABC. If we select an arbitrary point P inside the triangle, we can construct the segments AP, BP, and CP. We can then extend these segments until they intersect the sides of the triangle. We will label these intersections D, E, and F. We are interested in the values of (AF)(BD)(EC) and (FB)(DC)(EA).

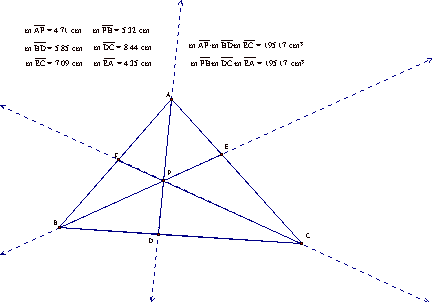
We can use the measure function in GSP to measure each segment of interest. Then we can use the calculator function to find the two products we are interested in. Notice that the two products are equal. Does this hold for other shapes of triangles?

Click here for a GSP file to try different shapes of triangles and different locations of P.

We see that these two products are indeed equal no matter the shape of the ABC and as long as P is inside ABC (for this construction).

If we construct ABC using lines instead of segments we can generalize out initial construction to show the value for the products even if P is outside of ABC.

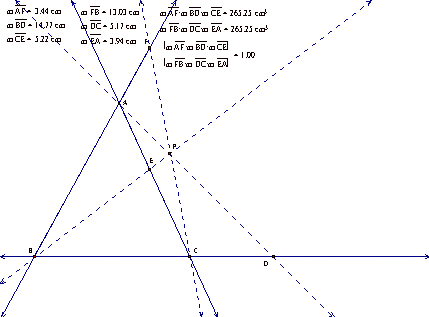
So we can see that (AF)(BD)(EC) = (FB)(DC)(EA) even when P is outside of triangle ABC.

Click here for a GSP file to try this for yourself.

Why is this so?

First lets construct a line parallel to BC that passes through A. This line intersects BE extended and CF extended at points I and H respectively.

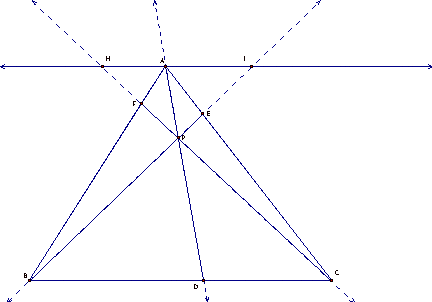
We now have a number of similar triangles. Triangle AIE is similar to ECB because corresponding angles are congruent (vertical angle and alternate interior angles). Triangle AHF is similar to BFC for the same reasons. Triangle APH is similar to DCP and API is similar to BDP also for the same reasons.

Because of these similar triangles we can conclude that the following ratios are equal:

AE/EC = AI/BC

BF/FA = BC/AH

AH/DC = AP/DP

AI/BD = AP/DP

These last two equalities imply that

AH/DC = AI/BD

(AH)(BD) = (AI)(DC)

AH/AI = DC/BD

So looking back at our products (AF)(BD)(EC) and (FB)(DC)(EA), if we divide one by the other and substitute the identities above we have

(AF/FB)*(BD/DC)*(EC/EA)

=(AH/BC)*(AI/AH)*(BC/AI)

=(AH*AI*BC)/(AH*AI*BC)

=1

We can go on to look at the ratio of the area of ABC to the area of triangle DEF when P is inside ABC.

We can again use the measure and calculator functions in GSP to examine the ratio of the area of ABC to the area of DEF for different shapes of triangles and different locations of P inside ABC.

Click here for a GSP file to try different shapes of triangles and locations of P yourself.

Notice that this ratio is always greater than or equal to 4 when P is inside ABC. If P is located at the centroid of ABC, then AD, BE, and CF are medians and DEF is the medial triangle of ABC. It is a property that the ratio of the area of any triangle and the area of its medial triangle is 4, since medial triangles have 1/4 the area of the larger triangle. Moving P to any other location inside ABC decreases the area of DEF. Thus the ratio of the area of ABC to the area of DEF is greater than or equal to 4 when P is inside ABC.