

The Problem: Interpret your graphs. What happens to
This is the case where b=1 and c=2 as a is varied.
Is there a common point to all of the graphs? What is it? What is the significance where a =0?
Do similar interpretations for other sets of graphs. How does the shape change? How does the position change?
First Let's look at a a few different graphs with different values of a.
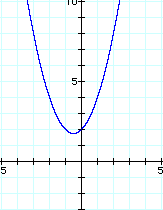
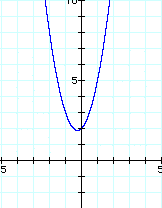
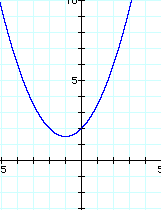
With these three graphs we notice that a large value of a seems to make the bowl-shape of the parabola narrower. The smaller value of a makes the bowl-shape wider. The vertex, or the minimum value, moves, yet the three parabolas all include the point (0, 2).
Now let's see what happens when a is negative.

With a negative a, we notice that the parabola has flipped over, but still the graph includes the point (0,2).
Now let's look at the case where a=0.
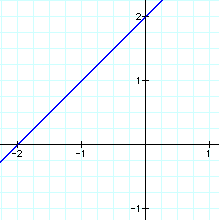
Since a =0, the term with the exponent = 2 ceases to exists. This gives us the equation y=x+2, which is not a quadratic, this finction is linear, meaning it graphs a line, as the graph above shows. We should still note that the point (0,2) is on the graph of the line.
Let's take a look at all of the graphs as a varies.
Click here to open a graph in graphing calculator 3.1
The next case that we need to look at is when a and b are fixed and c varies.
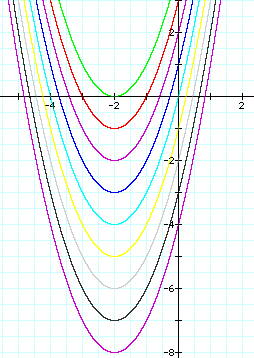
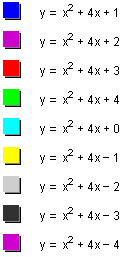
We can see here that the bowl-shape of the graph remains the same, but the graph is shifted up or down based on the value of c.
Now, let's look at the interesting case where b varies.
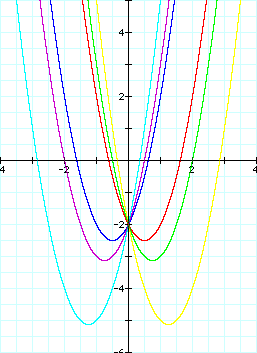
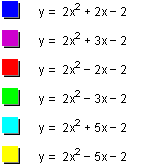
Varying values of b changes the location of the graph significantly, without changing the shape of the graph. Notice that all of the graphs go through the point (0,-2) which is implied by c=-2.
The vertices of the parabolas appear to be plotted along a parabolic curve. They appear to peak at the point (0,-2).
Click here to see a graph in graphing calculator 3.1
The equation for a parabola may be written in the form
where h and k are x and y values of the vertex, (h,k). So, in our example, h=0, and k=-2. We know that the parabola will open DOWN, so our value for a must be negative.
The points making this curve are the vertices from a family of parabolas with a=2.; it follows that the two are related. So, now we try:
Click here to see a graph in graphing calculator 3.1
Notice in the graph that the vertices of the verying parabolas follow the path with the eqation above.
Conjecture:
The vertices of the graph of
![]() as n varies,
as n varies,
will follow the parabolic path described by the equation
![]()