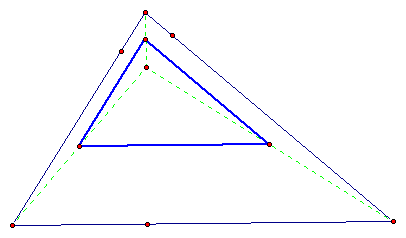
The orthocenter is the point of concurrency of the three altitudes of a triangle.
The third triangle is created by finding the orthocenter of our original triangle. The midponts of the segments whose endpoints are the orthocenter and the vertices of the original triangle form the vertices of this triangle.
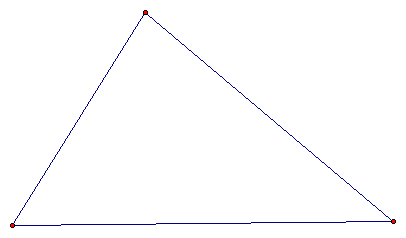
This is our original triangle. The first step is to find the orthocenter. To do this, we need to find the altitude of each side. The altitude is the perpendicular segment drawn from the vertex of a triangle to the line containing the opposite side of the triangle.
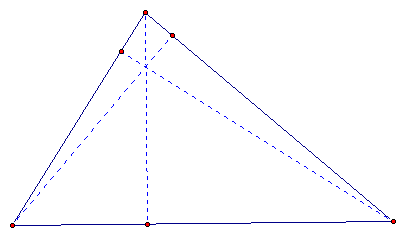
The dashed blue lines are our altitudes. Notice that they meet at a single point. This point is the orthocenter. Next we need to find the midpoints of the segments that connect the vertices with the orthocenter.
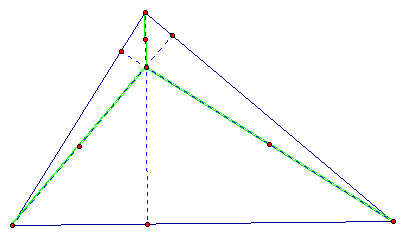
Those midpoints will be the the vertices of our new triangle. We need to connect the midpoints to draw the triangle.