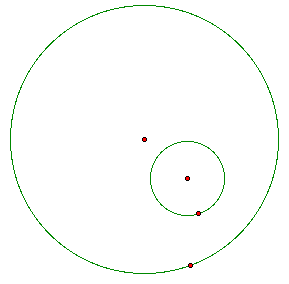
Case 1:

One circle is inside the other.

In this case, there are actually TWO different circles that will be tangent to our original circle.

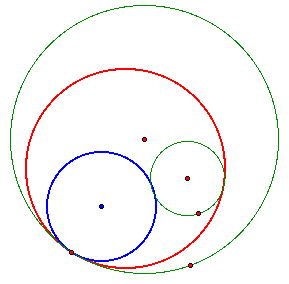
Let's look at the locus of all the centers of the tangent circles as the point of tangency moves along the larger circle.

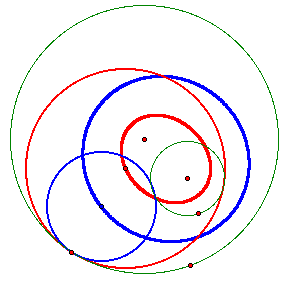
Notice that the loci are elipses whose foci are the centers of the original circles.

Click here to open a sketch in GSP to see the animation of the tangent circles' centers.

It can also be interesting to look at the envelope formed by tracing the the tangent lines.

Click here to see the the animation in GSP.

Click here to return to the Tangent Circles page.

Click here to continue to CASE TWO.

Click here to return to Julie's main page.