Given a circle and a line, construct the circle tangent to the circle (at an arbitrary point P) and the line.

Case 1: line and circle are disjoint

Case 2: line and circle intersect twice

These cases are very similar.

Notice that there are two circles that are tangent to both the circle and the line.

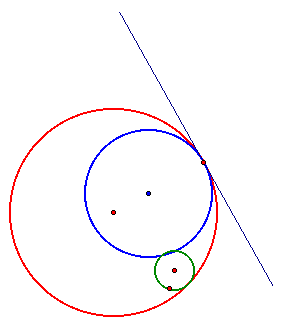
Let's look at the locus of the centers of the two tangent circles.

As we can tell from the picture for case 1, the locus is two parabolas.

Click here to see the animation in GSP.

It is also interesting to see the trace of the perpendicular lines.

Click here to see the animation of the perpendicular lines in GSP.

For case 2, the parabolas intersect.

Click here to open a sketch with an animation in GSP.

It would be interesting to know where the foci of the parabolas is. Is it the center of the circle? Is the line the directrix?

Click here for case 3.

Click here to return to Julie's main page.