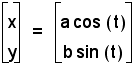
Let's explore

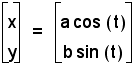
We have already examined the case where a = 1, and b = 1. This graphs the unit circle.

Let's begin with an examination of the effect a has on the graph.

First, let's consider the case where a = 2, and b = 1.

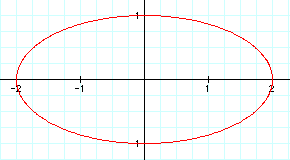
By changing the value of a to 2, the unit circle was stretched along the horizontal axis, creating an ellipse.

A value of a between 1 and 0, squashes the circle along the horizontal axis, creating an ellipse. Here is the case where a = 0.5, and b =1.

 

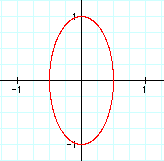
Now, let's look at the effect of b on the graph.

Here is the case where a = 1 and b = 2.

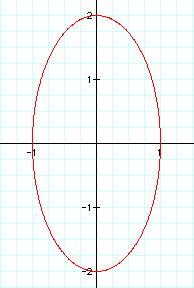
Again, the result is an ellipse. This time, b stretches the ellipse along the vertical axis.

A value of b between 1 and 0 will squash the curve along the vertical axis.

Here is the case where a = 1, and b = 0.5

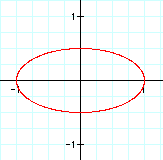
Different values of a and b can be combined to create different ellipses that have been stretched or squashed along both the vertical and horizontal axies.

Here is the graph where a = 3, and b = 0.5

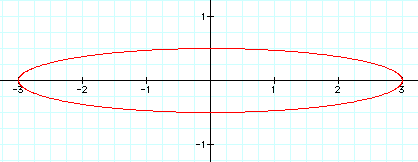
We have examined positive values of a and b. What do negative values of a and b do to the graph?

Here is the case where a = -3, and b = 1. The graph is identical to the case where a = 3, and b = 1.

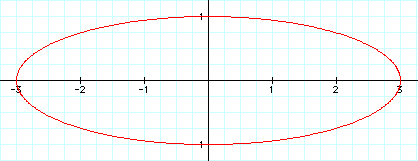
I believe that the graph was reflected in the vertical axis, but because the axis was also the axis of symmetry, the graph rests on top of itself.

 

Now, we need to examine the case where a or b is zero.

This is the case where a = 1, and b = 0.

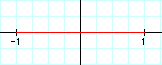
Notice that it is a segment that extends to 1 and -1 along the horizontal axis. A value of 0 for b, resutls in a segment along the horizontal axis.

 

This is the case where a = 0, and b = 1.

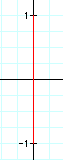
Notice that the segment extends to 1 and -1 along the vertical axis. A value of 0 for a results in a segment along the vertical axis.

Click here to return to the main Parametric Equations page.

Click here to return to Julie's main page