In the previous pages, we discussed the effects a had on the graph of
but, how much impact does it have on the graph
of ![]() ?
?

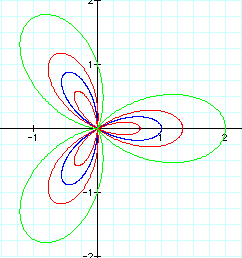
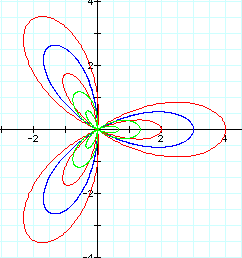
We can see from this layered graph that a value of a affects the size of the petals. The petals are much longer and wider when a does not equal zero.
Will a value of a that is less than 1 have the same effect? Meaning, will the petals be longer and wider, or will the petals, since the value is less than one, shrink?
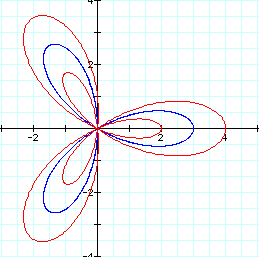
We can see that a value of (1/3) for a does not have the same effect, nor does it cause the petals to shrink. When a = 1/3, there are two sets of petals, one is larger and appears more rounded, but not as large and round as a value of a =1 created. The other set of petals is smaller and appears less rounded.
A similar graph is created by keeping a =1, but changing the value of b.
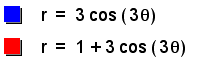
When a=o, but b=3, the petals
appear longer, but when a=1, and b=3, the result
is two sets of petals. This is similar to the graph of ![]()
Are those two graphs the same?
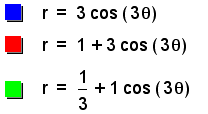
No, the graph of ![]() has
much larger petals than the graph of
has
much larger petals than the graph of ![]()
An extension to this problem would be to consider the areas enclosed by those two equations.
Is the area enclosed by the graph of
(1/3) of the area enclosed by the graph of
Click here to return to the Polar Equations main page.
Click here to return to Julie's main page.