What effect will b have if it is positive?
As a point of reference, below is the graph
of ![]()
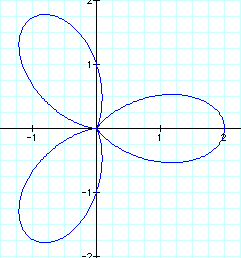
b>1
Now let's look at this same equation, but when b = 2.
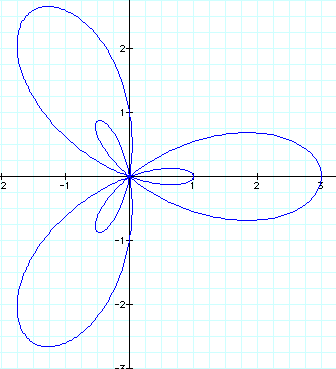
The first thing that we notice, is the second set of petals that are "nested" inside of the 3 petals. The petals have also been stretched or elongated.
When b=3, will there be 3 sets of petals?
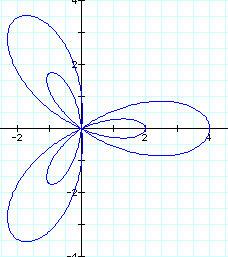
No, there remain only 2 sets of petals. But the petals are even longer.
So, the value of b greater than 1, creates a second set of petals, and stretches or elongates the petals.
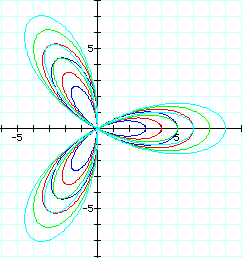
It is interesting, in this layered graph, there approaches a point when the tip of the interior petal (from the graph with a larger value of b) touches the tip of an exterior petal (from the graph with a smaller value of b).
What effect will b have if it is a fraction?
Here is the case where a=1, b=(1/3) and n=3.
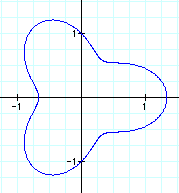
Notice, that b affects the graph similar to the way that a positive value for a might, by moving the graph farther from the origin.
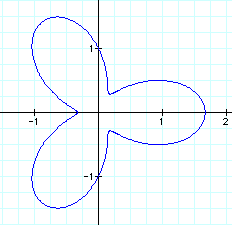
Notice in this case, where a = 1, n = 3, and b = (2/3), that the petals have more definition and gets closer to the origin, than the case where b=1/3.
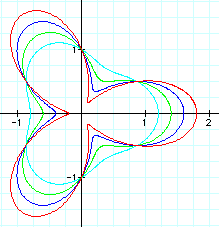
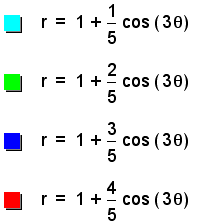
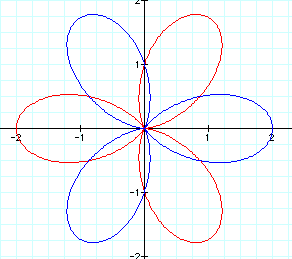
We can see from this layered graph, that the closer the value of b gets to 1, the longer the petals are, and the closer their bases get to the origin.
What effect will b have if it is negative?
A negative value for b simply reflects the graph across the vertical axis.
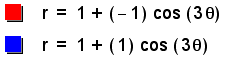
Click here to return to the Polar Equations main page.
Click here to return to Julie's main page.