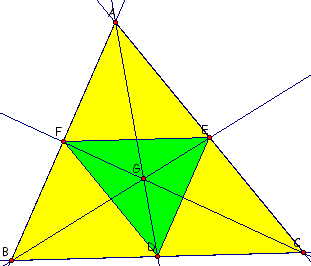
When will the ratio of the areas of the two triangles equal 4?

When triangle ABC is P is the pt of concurrency of the medians, the centroid, the ratio of the areas of the two triangles will be 4.

This is true because, since P is the centroid, F, D, and E are midpoints. This makes Triangle FDE the same size as Triangles AFE, FBD, and DEC. So, Triangle FDE makes up 1/4 the area of Triangle ABC.

Can there ever be a triangle DEF that is less than 1/4 the area of ABC?

Click here to open a GSP sketch to manipulate point P, and consider the ratio of the areas.

We can see in the GSP sketch that triangle ABC will always be at least 4 times larger than triangle DEF.

Notice that the farther the P gets from the centroid, that the larger the ratio of ABC to DEF gets.

Click here to return to the final main page.

Click here to return to Julie's main page.