Prove:

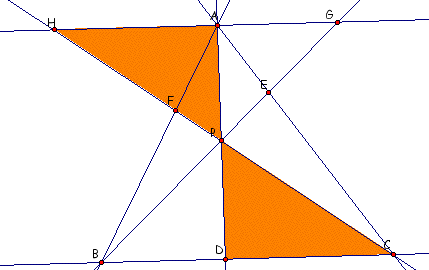
First, we create a line through A that is parallel to BC.

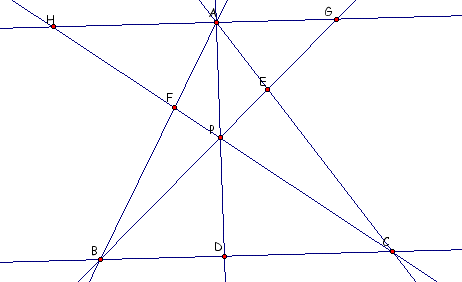
This allows us to look at several similar triangles and manipulate the properties of those similar triangles.

The first set of similar triangles is: triangle AHF and Triangle BCF.

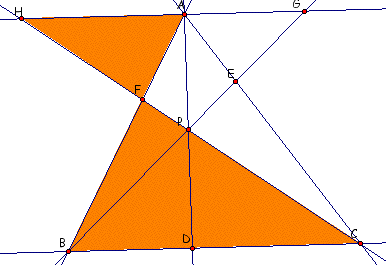
Corresponding sides of similar triangles have proportional sides. This allows us to look at the extended proportion:

The second set of similar triangles is: triangle AEG and triangle CEB.

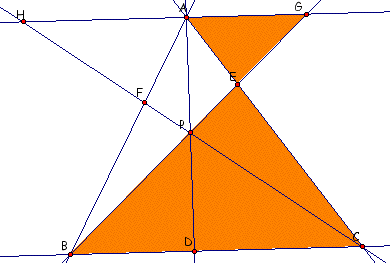
Here we look at the extended proportion:

Triangles AGP and DBP are also similar.

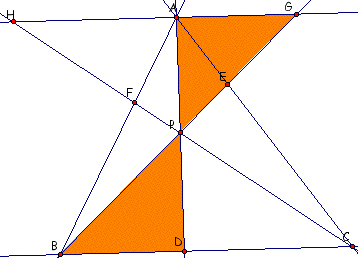
The proportion of the corresponding sides is:

And the last set of similar triangles that we need to look at is

triangle CDP and triangleHAP.

Here the proportion relating the sides is:

Using the last two proportions we see that:

and

Using the Transitive Property, we see that

Using the cross product property of proportions we can rewrite the proportion as:

So we have said:

Multiplying we see:

Which simplifies to:

This holds even when P is outside of the triangle, except when P is on one of the lines that include a vertex and are parallel to the opposite side of the triangle.

Click here to manipulate the GSP sketch.

Click here to return to the final main page.

Click here to return to Julie's main page.