by Rives Poe

Assignment 1:

Problems and explorations with graphing functions and relations.

Make up linear functions f(x) and g(x). Explore, with diffefent pairs of f(x) and g(x) the graphs for

i. h(x) = f(x) + g(x)

ii. h(x) = f(x).g(x)

iii. h(x) = f(x)/g(x)

iv. h(x) = f(g(x))

In this investigation we need two linear functions. Linear functions are functions that on their own form a line (hence the name linear!). For our purposes we will use the equations f(x)= x+1 and g(x)=-1/2x+5.

First let's see what these linear functions look like on their own.

 

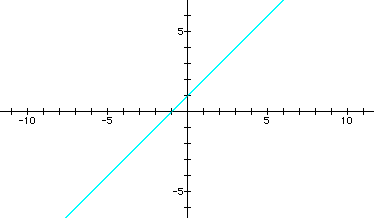f(x)=x+1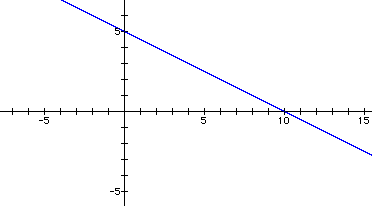g(x) = -1/2+5

 

 

If we tried h(x)=f(x)+g(x) what would you expect our graph to look like. Maybe there will be two lines in one coordinate plane, maybe not. Sketch down your ideas and then scroll down to see if you are right.

 

 

Here it is:

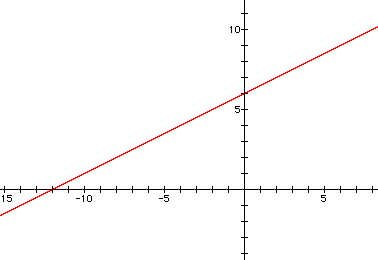
From this graph, it looks as though when you add two linear functions together you have a line. We could do the math if you need a little more proof:

If h(x)=f(x)+g(x), then h(x) = x+1 +(-1/2x +5). So h(x) = 1/2x+6. The y-intercept is y=6 and the x-intercept is x=-12. If you will remember the formula y=mx+b, it looks as though h(x) is in that same formula. "m" represents the slope and b is the y-intercept. The slope is positive m=1/2 and the function crosses the y-axis at y=6.

 

Let's see what will happen if we multiply g(x) by f(x).

h(x) = f(x)*g(x)

h(x) = (x+1)*(-1/2x+5)

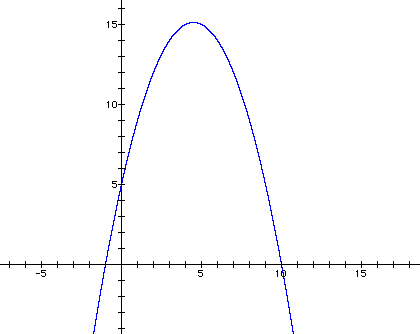
How can we explain why this graph looks different? What makes it non-linear? When we multiply the two equations together, we have h(x)=-1/2x^2-(1/2)x+5x+5. The first x value is now raised to the second power. From previous explorations we know that will create a parabola and because the coefficient is negative, the parabola is upside down.

 

What do you think will happen when we divide f(x) by g(X)? We know that the demominator cannot equal zero, so maybe two seperate graphs will form with an assymptote where g(x)=0.

h(x)=f(x)/g(x)

h(x) = (x+1)/(-1/2x+5)

Notice there is a vertical assymptote where x=10 and the equations form two slanted parabolas.

 

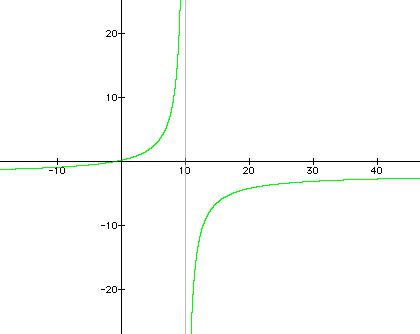
And last, but of course not least - let's look at h(x) = f(g(x)). We are evaluating f(x) where x=g(x).What do you expect the graph to look like in this case?

h(x) =((-1/2x+5)+1)

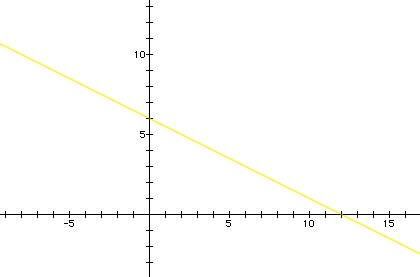
Were you correct? You should have expected a line with negative slope. When we work out the equation, h(x)=(-1/2)x+6. (remember: y=mx+b).

 

After working through this investigation, I hope you will feel comfortable looking at linear equations and predicting the graph.

 

Click here to explore these linear equations and create some of your own!

 

 

 

 

 

 

Return to home page