
Assignment 10
PARAMETRIC
CURVES
by Rives Poe
In this investigation,
we will look at parametric curves. A parametric curve in the plane
is a pair of functions
x=f(t) and y=g(t)
where the two continuous
functions define ordered pairs. The curve will depend on the range
of t . We are able to graph this type of equation
on Graphing Calculator easily.
We will start our investigation
looking at the graph of two parametric equations: x=cos(t) and
y=sin(t). We will have the range of t be from 0
to 2pi.
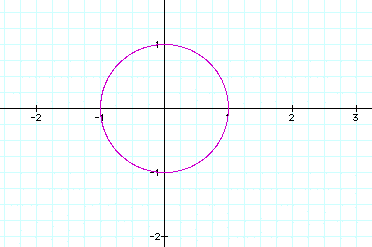 Because the two functions
define ordered pairs, we should have expected the curve to be
a circle. For example sin(0)=1 and c0s(0)=0, therefore the ordered
pair is (1,0), which we can see on the graph above.
Let's try changing the
equations to explore other graphs.
Because the two functions
define ordered pairs, we should have expected the curve to be
a circle. For example sin(0)=1 and c0s(0)=0, therefore the ordered
pair is (1,0), which we can see on the graph above.
Let's try changing the
equations to explore other graphs.
If we change the coefficient
of t, how do you think the graph will change? (I will not change
the range of t however -at least not yet!)
For example, let's look
at x=cos(at) and y=sin(bt). If we leave the a and b equal to 1,
we will have the same graph as above. What will happen if we set
a = 2 and b=2? Any ideas? Let's try it.
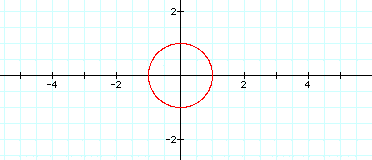 It is exactly the same
as the graph above. What if the coefficients are different? In
the next graph I will let a =1 and b=2. Let's see what happens.
It is exactly the same
as the graph above. What if the coefficients are different? In
the next graph I will let a =1 and b=2. Let's see what happens.
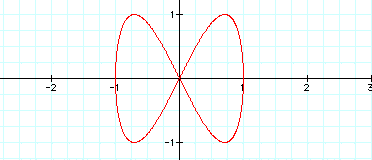 Now, that is different!
Before we decide what is happening let's lool at a couple more
curves.
For x=cos(at) and y=sin(bt),
let a = 2 and b=4:
Now, that is different!
Before we decide what is happening let's lool at a couple more
curves.
For x=cos(at) and y=sin(bt),
let a = 2 and b=4:
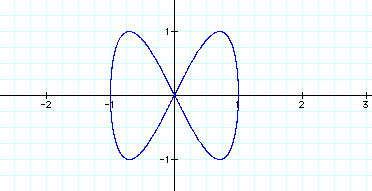 This graph looks the same
as when a=1 and b=2. Since a is half the value of b, the curve
crosses one time creating 2 areas.
Let's look at a=2 and b=6.
Since a is now 1/3 of b, I will conject that the curve will cross
two times, creating three areas. What do you think? Take a look!
This graph looks the same
as when a=1 and b=2. Since a is half the value of b, the curve
crosses one time creating 2 areas.
Let's look at a=2 and b=6.
Since a is now 1/3 of b, I will conject that the curve will cross
two times, creating three areas. What do you think? Take a look!
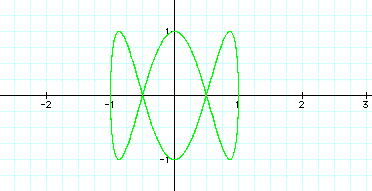 I was right! So, now we
have determined how to predict what happens when a is less than
b. What do you think will occur if b is less than a? Let's start
with something small, for example let a = 3 and b= 2.
I was right! So, now we
have determined how to predict what happens when a is less than
b. What do you think will occur if b is less than a? Let's start
with something small, for example let a = 3 and b= 2.
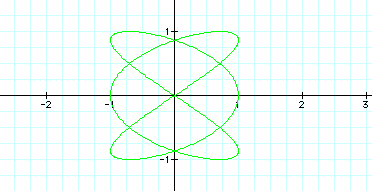 The curve crosses three
times along the y-axis, which equals the value of a.
When a is greater than
b, the curve seems to graph on the y-axis. When b is greater than
a, the curve seems to graph along the x-axis.
To investigate more with
these two parametric equations, click here .
The curve crosses three
times along the y-axis, which equals the value of a.
When a is greater than
b, the curve seems to graph on the y-axis. When b is greater than
a, the curve seems to graph along the x-axis.
To investigate more with
these two parametric equations, click here .
Let's investigate what
happens if we multiply the two equations by a and b.
x=a cos(t)
y=b sin(t)
If we set a and b equal
to 1, then we will have the same graph as our very first one.
What do you think is going to happen when we let a and b equal
2? Take a look:
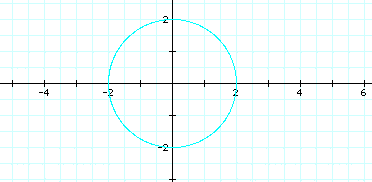 So, as long as a and b
are equal, (in all of the cases above) the two equations will
create a circle.
Now try a=2 and b=3:
So, as long as a and b
are equal, (in all of the cases above) the two equations will
create a circle.
Now try a=2 and b=3:
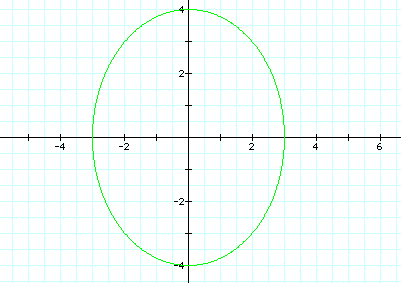
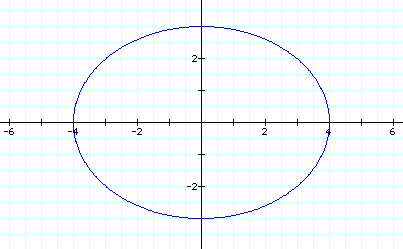 When a is greater than
b, an ellipse is formed. When a is less than b, an ellipse will
also be created, but on the y-axis. In the following graph, a=3
and b=4
When a is greater than
b, an ellipse is formed. When a is less than b, an ellipse will
also be created, but on the y-axis. In the following graph, a=3
and b=4
 To investigate more with
parametric curves for the equations x=a cos(t) and y=b sin(t),
click
here.
To investigate more with
parametric curves for the equations x=a cos(t) and y=b sin(t),
click
here.
RETURN
to home page










